Method Article
機械学習モデルに基づく大腸印指輪癌における3リンパ節病期分類システムの予測性能の比較
要約
この研究では、機械学習モデルと競合するリスク分析を使用して、結腸直腸記号リング細胞癌患者の予後システムを評価します。これは、pN病期分類と比較して優れた予測因子として陽性リンパ節の対数オッズを特定し、強力な予測パフォーマンスを示し、堅牢な生存予測ツールを通じて臨床上の意思決定を支援します。
要約
リンパ節の状態は、患者にとって重要な予後予測因子です。しかし、結腸直腸標識リング細胞がん(SRCC)の予後については、あまり注目されていません。この研究では、機械学習モデル (Random Forest、XGBoost、Neural Network) と競合するリスク モデルを使用して、SRCC 患者における陽性リンパ節 (LODDS)、リンパ節比 (LNR)、および pN 病期分類の対数オッズの予後予測能力を調査します。関連データは、Surveillance, Epidemiology, and End Results(SEER)データベースから抽出した。機械学習モデルでは、単変量および多変量Cox回帰分析を通じてがん特異的生存(CSS)の予後因子を特定し、その後、XGBoost、RF、NNの3つの機械学習手法を適用して、最適なリンパ節病期分類システムを確認しました。競合リスクモデルでは、予後因子を特定するために単変量および多変量競合リスク分析が採用され、SRCC患者の予後を予測するためにノモグラムが構築された。レシーバー動作特性曲線(AUC-ROC)および較正曲線の下の面積は、モデルのパフォーマンスを評価するために利用されました。この研究には、合計2,409人のSRCC患者が含まれていました。モデルの有効性を検証するために、SRCC症例を除く15,122人の結腸直腸がん患者の追加コホートを外部検証に含めました。機械学習モデルと競合するリスクノモグラムは、生存結果の予測において優れたパフォーマンスを示しました。pN病期分類と比較して、LODDS病期分類システムは優れた予後能力を示しました。評価の結果、機械学習モデルと競合するリスクモデルは、優れた識別、キャリブレーション、および解釈可能性を特徴とする優れた予測パフォーマンスを達成しました。私たちの調査結果は、患者の臨床的意思決定に情報を提供するのに役立つ可能性があります。
概要
結腸直腸癌(CRC)は、世界で3番目に多い悪性腫瘍としてランク付けされています1,2,3。印環細胞がん(SRCC)は、CRCのまれな亜型であり、症例の約1%を占め、細胞核1,2,4を置換する細胞内ムチンが豊富にあることを特徴としています。SRCCは、若年患者と関連していることが多く、女性の有病率が高く、診断時の腫瘍病期が進行しています。結腸直腸腺癌と比較して、SRCCは分化が不十分で、遠隔転移のリスクが高く、5年生存率はわずか12%〜20%です5,6。SRCCの正確で効果的な予後モデルを開発することは、治療戦略を最適化し、臨床転帰を改善するために重要です。
この研究は、機械学習 (ML) や競合するリスク モデルなどの高度な統計的アプローチを使用して、SRCC 患者の堅牢な予後モデルを構築することを目的としています。これらの方法論は、臨床データの複雑な関係に対応でき、個別のリスク評価を提供し、予測精度で従来の方法を凌駕します。Random Forest、XGBoost、Neural Networksなどの機械学習モデルは、高次元データの処理と複雑なパターンの識別に優れています。研究によると、AIモデルは結腸直腸がんの生存転帰を効果的に予測し、臨床応用におけるMLの可能性を強調しています7,8。MLを補完する競合するリスクモデルは、がん特異的な死亡率と他の死因など、複数のイベントタイプに対処し、生存分析を改善します。Kaplan-Meier推定量のような従来の方法とは異なり、競合するリスクモデルは、競合するリスクが存在する場合の事象の限界確率を正確に推定し、より正確な生存評価を提供する8。MLと競合するリスク分析を統合することで、予測パフォーマンスが向上し、SRCC 9,10,11のパーソナライズされた予後ツールの強力なフレームワークが提供されます。
リンパ節転移は、CRC患者の予後と再発に大きく影響します。TNM分類におけるNステージ評価は重要ですが、不十分なリンパ節検査(症例の48%〜63%で報告されています)は、疾患の過小評価につながる可能性があります。これに対処するために、リンパ節比(LNR)や陽性リンパ節の対数オッズ(LODDS)などの代替アプローチが導入されています。LNRは、陽性リンパ節(PLN)と全リンパ節(TLN)の比率であり、TLN数の影響を受けにくく、CRCの予後因子として機能します。LODDSは、PLNと陰性リンパ節(NLN)の対数比であり、胃SRCCと結腸直腸癌の両方で優れた予測能力を示しています10,11。機械学習は腫瘍学でますます適用されており、モデルは乳がん、前立腺がん、肺がんなどのさまざまながんのリスク層別化と予後予測を改善しています12,13,14。ただし、結腸直腸SRCCへの適用は依然として限られています。
この研究では、LODDSをMLおよび競合するリスクモデルと統合して包括的な予後ツールを作成することにより、このギャップを埋めることを目指しています。この研究は、LODDSの予後的価値を評価し、高度な予測技術を活用することにより、SRCC患者の臨床的意思決定を強化し、転帰を改善することを目的としています。
プロトコル
この研究は、倫理的な承認と参加の同意を指すものではありません。この研究で使用されたデータは、データベースから取得されました。2004年から2015年に結腸直腸標識リング細胞がんと診断された患者、および他の種類の結腸直腸がんの患者を含めました。除外基準は、生存期間が1ヵ月未満の患者、臨床病理学的情報が不完全な患者、死因が不明または特定されていない症例であった。
1. データ取得
- SEERをダウンロードします。SEERデータベースWebサイト(http://seer.cancer.gov/about/overview.html)から統計8.4.3ソフトウェアを入手します。ソフトウェアにログインした後、[Case List Session] >データと 発生 率SEERリサーチプラスデータ、17レジストリ、2021年11月サブ(2000-2019)データベースを選択します。
- [選択] > [編集] をクリックし、{人種、性別、年、Dx. 診断年} = '2004', '2005', '2006', '2007', '2008', '2009', '2010', '2011', '2012', '2013', '2014', '2015' AND {サイトと形態を選択します。サイト再コードICD-O-3 / WHO 2008} = '8490/3'。
- 次に、[ テーブル]をクリックし、使用可能な変数インターフェイスで、[ 単一の年齢と100+の年齢再コード]、[性別]、[婚姻]、[サイト再コードICD-O-3 / WHO 2008]、[CS腫瘍サイズ]、[地域nodes_examined(1988+)]、[地域nodes_positive(1988+)]、[派生AJCCステージグループ、第6版(2004-2015)]、[派生AJCC T、第6版(2004-2015)]、[派生AJCC M]、[ 第6版(2004-2015)、CEA、放射線再コード、化学療法再コード(はい、いいえ/unk)、SEER原因別死亡分類、バイタルステータス再コード(研究カットオフを使用)、生存月、 診断年。
- 最後に、[ 出力]をクリックし、データに名前を付け、[ 実行 ]をクリックしてデータを出力して保存します。詳細なインクルージョンプロセスを 図1に示します。
- 結腸直腸がん患者(SRCC症例を除く)のデータをダウンロードして、その後の外部検証に利用できます。[選択] > [編集] をクリックし、{人種、性別、年、Dx. 診断年} = '2004'、'2005'、'2006'、'2007'、'2008'、'2009'、'2010'、'2011'、'2012'、'2013'、'2014'、'2015'、{プライマリ サイト - ラベル付き} = 'C18-C20' を選択します。手順 1.3 と 1.4 を繰り返して臨床病理情報を取得し、{Site and Morphology を持つサンプルを除外します。ダウンロードしたファイルからICD-O-3/WHO 2008} = '8490/3'をサイト再コードします。
- 比較のために、いくつかの変数を処理します。リンパ節比(LNR)と陽性リンパ節のオッズの対数(LODDS)の両方を使用して、リンパ節の状態を分類します。
- LNRは、陽性リンパ節(PLN)と全リンパ節(TLN)の比率として定義します。次の式を使用して LODDS 値を計算します。
loge(PLNの数 + 0.5) / (陰性リンパ節(NLN)の数 + 0.5)
ここで、0.5 は無限の結果を防ぐために追加されました。LNR、LODDS、および腫瘍サイズのカットオフ値は、最小P値法に基づいてX-tileソフトウェア(バージョン3.6.1)を使用して決定されました。
- LNRは、陽性リンパ節(PLN)と全リンパ節(TLN)の比率として定義します。次の式を使用して LODDS 値を計算します。
- X-tileソフトウェアを開き、[ ファイル]>[開く]をクリックし、データファイルを選択してソフトウェアにインポートします。データが読み込まれたら、変数をマッピングします: Censor は生存状態に対応し、Survival time は生存時間に対応し、marker1 は分析対象の変数で、データが正しく一致することを確認します。
- 次に、「 Do > Kaplan-Meier > Marker1 」をクリックして、Kaplan-Meier生存分析を実行し、生存曲線を生成します。Kaplan-Meier生存曲線の分離、統計的有意性(p値など)、および臨床的関連性に基づいて、最適なカットオフ値を決定し、最終的に分析結果を記録またはエクスポートします。
- LNRをLNR 1(≤0.16)、LNR 2(0.16 - 0.78)、LNR 3(≥ 0.78)の3つのグループに分けます。LODDS に基づいて、患者を LODDS 1 (≤ -1.44)、LODDS 2 (-1.44 - 0.86)、LODDS 3 (≥ 0.86) の 3 つのグループに分類します。
- 腫瘍のサイズを 3.5 cm ≤、3.5 - 5.5 cm、5.5 cm ≥ の 3 つのカテゴリに分類します。年齢を連続変数からカテゴリ変数に変換します。初期診断時の患者の年齢を≥60歳と<60歳に分類します。印環細胞がん(SRCC)腫瘍の分布に基づいて、腫瘍の位置を右結腸、左結腸、および直腸に分類します。右結腸には、盲腸、上行結腸、肝屈曲、横行結腸が含まれ、左結腸には、脾屈、下行結腸、S状結腸、および直腸S状結腸が含まれます。
- この研究では、SRCC を使用して合計 2409 人の適格な患者データを、トレーニング コホート (N = 1686) と検証コホート (N = 723) に 7:3 の比率でランダムに割り当てます。ランダム分割と SEER データベースからのソースdata.csvには、次のコードを使用します。ランダム分割後に生成されたファイルは、さらなる分析に使用されます。
図書室(キャレット)
データ<-read.csv(以下「data.csv」)
セットシード(123)
train_indices <- createDataPartition(data$variable, p = 0.7, list = FALSE)
train_data <- データ[train_indices, ]
test_data <- データ[-train_indices, ]
write.csv(train_data, "traindata.csv", row.names = FALSE)
write.csv(test_data, "testdata.csv", row.names = FALSE)
2. MLモデルの開発と検証
- RStudio (2024.04.2+764) と R ソフトウェア (4.4.1) をダウンロードします。RStudio を開いて R ソフトウェアを実行します。 [新しいファイル ]をクリックし、[ Rスクリプト ]を選択して、新しいRプログラミングインターフェイスを作成します。コードエディタで関連するコードを入力し、[ 実行 ]をクリックしてコードを実行します。
- 次のコードを使用して、Cox 回帰分析によって ML モデルに含まれる変数をスクリーニングします。さらに、SRCC患者のがん特異的生存期間(CSS)に対するLODDS、LNR、およびpN病期分類の影響を調査します。traindata.csvは、SEERデータベースから取得したデータです。
library("サバイバル")
ライブラリ("survminer")
ライブラリ("rms")
ライブラリ("dplyr")
データ <- read.csv(以下「traindata.csv」といいます。
data$time=as.numeric(data$time)
data$status=as.numeric(data$status)
変数 <- c("性別", "年齢", "人種", "夫婦", "ステージ", "T", "N", "M","Tumor_size", "LNR", "LODDS", "CEA","放射線", "化学療法", "サイト")
data <- data %>%
mutate(across(all_of(変数), as.factor))
cox=coxph(Surv(時間, ステータス) ~ data$T, data = data)
cox$coefficients
pval=anova(cox)$Pr[2]
clean_data=データ[,c(1:12, 14:18)]
get_coxVariable=関数(your_data,インデックス){cox_list=c() k=1
for (i in 1:index) {mod=coxph(Surv(time, status) ~ your_data[,i],data=your_data) pval=anova(mod)$Pr[2] print:pval) print(your_data)[i]) if ) (pval<0.05) {cox_list[k]=colnames(your_data)[i] k=k+1}}returncox_list)))
variable_select=get_coxVariable(clean_data,15)
for(i in 1:15){print(variable_select[i])}
for (var in variable_select) {formula <- as.formula(paste("Surv(時間, ステータス) ~", var)))cox_model <- coxph)(formula, data = data) print(summary)cox_model))
GGフォレスト(COX)
変数 <- c("性別", "年齢", "人種", "夫婦", "ステージ", "T", "N", "M", "Tumor_size", "LNR", "LODDS", "化学療法")
data <- data %>%
mutate(across(all_of(変数), as.factor))
cox=coxph(Surv(時間, ステータス) ~ 性別+年齢+人種+婚姻+T+N+M+Tumor_size+LNR+
LODDS+化学療法、データ=データ)
ggforest(cox,data = data)
ggplot_forest <- ggforest(cox, data = data) - 次のコードを使用して、トレーニング、検証、および外部検証のコホート間で 3 つの LN システム (LODDS、LNR、pN ステージング) の予後予測能力を比較します。
図書館(RMS)
図書館(サバイバル)
図書館(survminer)
ライブラリ(riskRegression)
ライブラリ(GT)
train_data <- read.csv(以下「train_data123.csv」)
validation_data <- read.csv(以下「test_data123.csv」)
DD <- データディスト(train_data)
options(datadist = "dd")
model_LNR <- cph(Surv(時間, ステータス) ~ LNR, data = train_data, x = TRUE, y = TRUE)
model_LODDS <- cph(Surv(時間, status) ~ LODDS, データ = train_data, x = TRUE, y = TRUE)
model_pN <- cph(Surv(時間, ステータス) ~ N, データ = train_data, x = TRUE, y = TRUE)
calculate_performance <- function(model, data) {pred <- predict(model, newdata = data) c_index_result <- concordance(Surv(data$time, data$status) ~ pred) c_index <- c_index_result$concordance aic <- AIC(model) bic <- BIC(model) return)c) c(C_index = round(c_index, 3), AIC = round(aic) 2)、BIC = round%(bic% 2))}
calculate_performance <- function(model, data) {pred <- predict(model, newdata = data, type = "lp") concordance_result <- concordancefit(Surv(data$time, data$status), x = pred) c_index <- concordance_result$concordance ci_lower <- c_index - 1.96 * sqrt(concordance_result$var) ci_upper <- c_index + 1.96 * sqrt(concordance_result$var) AIC <- AIC(model) bic <- BIC(model) return(c(C_Index = round(c_index, 3), CI_Lower = round(ci_lower, 3), CI_Upper = round(ci_upper, 3), AIC = round(aic, 2), BIC = round(bic, 2))}
train_LNR <- calculate_performance(model_LNR年、train_data年)
train_LODDS <- calculate_performance(model_LODDS, train_data)
train_pN < - calculate_performance(train_data年、model_pN年)
model_LNR_val <- cph(Surv(時間, ステータス) ~ LNR, データ = validation_data, x = TRUE, y = TRUE)
model_LODDS_val <- cph(Surv(time, status) ~ LODDS, data = validation_data, x = TRUE, y = TRUE)
model_pN_val <- cph(Surv(時間, ステータス) ~ N, データ = validation_data, x = TRUE, y = TRUE)
val_LNR <- calculate_performance(model_LNR_val, validation_data)
val_LODDS < - calculate_performance(model_LODDS_val、validation_data)
val_pN < - calculate_performance(model_pN_val, validation_data)
結果 <- data.frame(Variable = c("LNR", "LODDS", "pN"), Training_C_Index = c(paste(train_LNR["C_Index"], "(", train_LNR["CI_Lower"], ", ", train_LNR["CI_Upper"], ")", sep = ""), paste(train_LODDS["C_Index"], "(", train_LODDS["CI_Lower"], ", ", train_LODDS["CI_Upper"], ")", sep = ""), paste(train_pN["C_Index"], "(", train_pN["CI_Lower"], ", ", train_pN["CI_Upper"], ")", sep = "")), Training_AIC = c(train_LNR["AIC"], train_LODDS["AIC"], train_pN["AIC"]), Training_BIC = c(train_LNR["BIC"], train_LODDS["BIC"], train_pN["BIC"]), Validation_C_Index = c(paste(val_LNR["C_Index"], "(", val_LNR["CI_Lower"], ", ", val_LNR["CI_Upper"], ")", sep = ""), paste(val_LODDS["C_Index"], "(", val_LODDS["CI_Lower"], ", ", val_LODDS["CI_Upper"], ")" sep = ""), paste(val_pN["C_Index"], "(", val_pN["CI_Lower"], ", ", ", val_pN["CI_Upper"], ")", sep = "")), Validation_AIC = c(val_LNR["AIC"], val_LODDS["AIC"], val_pN["AIC"]), Validation_BIC = c(val_LNR["BIC"], val_LODDS["BIC"], val_pN["BIC"]))
results_table <- gt(結果) %>%
tab_header(title = "3つのリンパ節の病期分類システムの予測性能") %>%
cols_label(変数 = "変数",Training_C_Index = "C-index (95% CI) (Training)", Training_AIC = "AIC (Training)", Training_BIC = "BIC (Training)", Validation_C_Index = "C-index (95% CI) (Validation)", Validation_AIC = "AIC (Validation)", Validation_BIC = "BIC (Validation)")
write.csv(results, "prediction_performance.csv", row.names = FALSE) - 次のコードを使用して XGBoost モデルを作成し、変数の相対的な重要度の棒グラフを生成することで、3 つの LN システムの重要度を比較します。同様に、ROC曲線と検量線を生成します。データはSEERデータベースから取得されます。
ライブラリ(XGBOOST)
図書室(キャレット)
図書館(pROC)
train_data <- read.csv(「train_data.csv」)
test_data <- read.csv(「test_data.csv」)
train_matrix < - xgbの。DMatrix(data = as.matrix(train_data[, c('Age', 'T', 'N', 'M', 'LODDS', 'Chemotherapy')]), label = train_data$status)
test_matrix < - xgbです。DMatrix(data = as.matrix(test_data[, c('Age', 'T', 'N', 'M', 'LODDS', 'Chemotherapy')]), label = test_data$status)
params <- list(booster = "gbtree", objective = "binary:logistic", eval_metric = "auc", eta = 0.1, max_depth = 6, subsample = 0.8, colsample_bytree = 0.8)
xgb_model <- xgb.train(params = params, data = train_matrix, nrounds = 100, watchlist= list(train = train_matrix), verbose = 1)
pred_probs <- predict(xgb_model, newdata = test_matrix)
pred_labels <- ifelse(pred_probs > 0.5, 1, 0)
conf_matrix <- confusionMatrix(as.factor(pred_labels), as.factor(test_data$status))
roc_curve <- roc(test_data$status, pred_probs)
auc_value <- AUC(roc_curve)
ci_auc <- CI.AUC(roc_curve)
感度 <- conf_matrix$byClass["感度"]
特異度 <- conf_matrix$byClass["特異度"]
精度 <- conf_matrix$overall["精度"]
ppv <- conf_matrix$byClass["位置予測値"]
npv <- conf_matrix$byClass["負の予測値"]
result_table <- data.frame(モデル = "XGBoost", AUC = sprintf("%.3f (%.3f-%.3f)", auc_value, ci_auc[1], ci_auc[3]), 感度 = sprintf("%.3f", 感度), 特異度 = sprintf("%.3f", 特異度), 精度 = sprintf("%.3f", 精度), PPV = sprintf("%.3f", ppv), NPV = sprintf("%.3f", npv))
write.csv(result_table, "xgboost_model_performance.csv", row.names = FALSE)
roc_df <- data.frame(FPR = 1 - roc_curve$specificities, TPR = roc_curve$sensitivities)
roc_plot <- ggplot(roc_df, aes(x = FPR, y = TPR)) +geom_line(color = "steelblue", size = 1.2) + geom_abline(intercept = 0, slope = 1, linetype = "破線", color = "gray") + annotate("text", x = 0.9, y = 0.2, label = paste("AUC =", round(auc_value, 3)), size = 5, color = "黒") + labs(title = "XGBoost モデルのROC曲線", x = "偽陽性率", y = "真陽性率") + theme_minimal() + theme(panel.border = element_rect(color = "黒", fill = NA, size = 1))
calibration_data <- data.frame(Status = as.factor(test_data$status), pred_probs = pred_probs)
calib_model <-キャリブレーション(ステータス~pred_probs、データ= calibration_data、クラス= "1"、カット= 5)
ggplot(calib_model$data, aes(x = 中点, y = パーセント)) + geom_line(color = "steelblue", size = 1) + geom_point(color = "red", size = 2) + geom_abline(切片 = 0, 傾き = 1, 線種 = "破線", color = "黒") +labs(title = "XGBoost モデルの検量線", x = "予測確率", y = "観測された比率") + theme_minimal() + theme(panel.border = element_rect(color = "黒", fill = NA, size = 0.5)) - 次のコードを使用して RF モデルを作成し、変数の相対的な重要度の棒グラフを生成して、3 つの LN システムの重要度を比較します。同様に、ROC曲線と検量線を生成します。データはSEERデータベースから取得されます.library(randomForest)
図書室(dplyr)
ライブラリ(ggplot2)
図書館(pROC)
図書室(キャレット)
図書館(RMS)
トレインセット<-read.csv(以下「train_data.csv」)
テスト済み <- read.csv(以下「test_data.csv」)
trainset$status=factor(トレインセット$status)
変数1 <- c("年齢", "T", "N", "M", "LODDS", "化学療法")
トレインセット <- トレインセット %>%
mutate(across(all_of(変数1), as.numeric))
testsed$status=factor(テストされた$status)
テスト済み <- テスト済み %>%
mutate(across(all_of(変数1), as.numeric))
RF=randomForest(trainset$status ~ 年齢 + T + N + M + LODDS + 化学療法, data=trainset,ntree=100,importance=TRUE,proximity=TRUE)
imp=重要度(RF)
変数インププロット(RF)
impvar=rownames(imp)[order(imp[,4],decreasing = TRUE〕
importance_df <- as.data.frame(imp)
importance_df$Variables <- rownames(importance_df)
importance_plot <- ggplot(importance_df, aes(x = reorder(Variables, MeanDecreaseAccuracy), y = MeanDecreaseAccuracy)) +geom_bar(stat = "identity", fill = "steelblue") +coord_flip() + labs(title = "変数の重要度", x = "変数", y = "平均低下精度") + theme_minimal()
pred_probs <- predict(RF, testset, type = "prob")[,2]
roc_obj <- roc(testset$status, pred_probs)
auc_value <- AUC(roc_obj)
roc_plot <- ggplot() +geom_line(aes(x = 1 - roc_obj$specificities, y = roc_obj$sensitivities), color = "steelblue", size = 1.2) +geom_abline(intercept = 0, slope = 1, linetype = "破線", color = "gray") + annotate("text", x = 0.8, y = 0.2, label = paste("AUC =", round(auc_value, 3)), color = "black", size = 5, hjust = 0) + labs(title = "ランダムフォレストモデルのROC曲線", x = "偽陽性率", y = "真陽性率") +theme_minimal() + theme(panel.border = element_rect(color = "黒", fill = NA, size = 1))
calibration_data <- data.frame(pred_probs = pred_probs, status = testsed$status)
calib_model <-キャリブレーション(ステータス~pred_probs、データ= calibration_data、クラス= "1"、カット= 5)
calib_df <- as.data.frame(calib_model[["データ"]])
calib_df$mid <- calib_df$midpoint
calib_df$パーセント <- calib_df$パーセント
calibration_plot <- ggplot(calib_df, aes(x = mid, y = Percent)) + geom_line(color = "steelblue", size = 1.2) + geom_point(color = "steelblue", size = 3) + geom_abline(intercept = 0, slope = 1, linetype = "破線", color = "黒", size = 0.8) + labs(title = "ランダムフォレストの検量線", x = "予測確率", y = "実際の確率") + theme_minimal() + theme(panel.border = element_rect(color = "黒", fill = NA, size = 1), plot.title = element_text(hjust = -0.05, vjust = -1.5, face = "bold", size = 12))
rf_probs <- predict(RF, newdata=testsed, type="prob")[, 2]
rf_auc <- roc(テスト済み$status, rf_probs)
auc_value <- AUC(rf_auc)
ci_auc <- CI.AUC(rf_auc)
rf_predictions <- predict(RF, newdata=testsed)
conf_matrix <- confusionMatrix(rf_predictions, testsed$status)
感度 <- conf_matrix$byClass["感度"]
特異度 <- conf_matrix$byClass["特異度"]
精度 <- conf_matrix$overall["精度"]
ppv <- conf_matrix$byClass["位置予測値"]
npv <- conf_matrix$byClass["負の予測値"]
result_table <- data.frame(モデル = "RF", AUC = sprintf("%.3f (%.3f-%.3f)", auc_value, ci_auc[1], ci_auc[3]), 感度 = sprintf("%.3f", 感度), 特異度 = sprintf("%.3f", 特異度), 精度 = sprintf("%.3f", 精度), PPV = sprintf("%.3f", ppv), NPV = sprintf("%.3f", npv))
write.csv(result_table, "RF_model_performance.csv", row.names = FALSE) - 次のコードを使用して NN モデルを作成し、変数の相対的な重要度の棒グラフを生成して、3 つの LN システムの重要度を比較します。同様に、ROC曲線と検量線を生成します。データは SEER データベースから取得されます。library(nnet)
図書室(キャレット)
図書館(pROC)
ライブラリ(ggplot2)
train_data <- read.csv(「train_data.csv」)
test_data <- read.csv(「test_data.csv」)
train_data$status <- as.factor(train_data$status)
test_data$status <- as.factor(test_data$status)
特徴 <- c("年齢", "T", "N", "M", "LODDS", "化学療法")
x_train <- train_data[、機能]
y_train <- train_data$status
x_test <- test_data[、特徴]
y_test <- test_data$status
nn_model <- nnet(ステータス ~ 年齢 + T + N + M + LODDS + 化学療法、データ = train_data、サイズ = 5、崩壊 = 0.01、最大値 = 200)
pred_probs <- predict(nn_model, newdata = x_test, type = "raw")
pred_labels <- ifelse(pred_probs > 0.5, 1, 0)
roc_curve <- ROC(数値(y_test), pred_probs)
auc_value <- AUC(roc_curve)
auc_ci <- CI.AUC(roc_curve)
auc_text <- paste0(round(auc_value, 3), " (", round(auc_ci[1], 3), "-", round(auc_ci[3], 3), ")")
conf_matrix <- confusionMatrix(as.factor(pred_labels), y_test)
精度 <- conf_matrix$overall["精度"]
感度 <- conf_matrix$byClass["感度"]
特異度 <- conf_matrix$byClass["特異度"]
ppv <- conf_matrix$byClass["位置予測値"]
npv <- conf_matrix$byClass["負の予測値"]
performance_table <- data.frame(Metric = c("AUC (95% CI)", "Accuracy", "Sensitivity", "Specificity", "PPV", "NPV"),Value = c(auc_text, round(精度, 3), round(感度, 3), round(特異度, 3), round(ppv, 3), round(npv, 3)))
write.csv(performance_table, "NN_performance_table.csv", row.names = FALSE)
roc_curve < - ROC(y_test, pred_probs)
auc_value <- AUC(roc_curve)
roc_plot <- ggplot() + geom_line(aes(x = 1 - roc_curve$specificities, y = roc_curve$sensitivities), color = "steelblue", size = 1.2) +geom_abline(intercept = 0, slope = 1, linetype = "破線", color = "gray") + annotate("text", x = 0.8, y = 0.2, label = paste("AUC =", round(auc_value, 3)), color = "black", size = 5, hjust = 0) + labs(title = "ニューラルネットワークモデルのROC曲線", x = "偽陽性率", y = "真陽性率") + theme_minimal() + theme(panel.border = element_rect(color = "black", fill = NA, size = 1))
calibration_data <- data.frame(pred_probs = pred_probs, status = as.numeric(y_test) - 1)
calibration_data$pred_probs <- as.numeric(calibration_data$pred_probs)
calibration_data$calibration_bin <- cut(calibration_data$pred_probs, breaks = seq(0, 1, by = 0.2), include.lowest = TRUE)
calibration_summary <集計(ステータス~calibration_bin、データ=calibration_data、FUN=平均)
calibration_summary$pred_mean <- 集計(pred_probs ~ calibration_bin, データ = calibration_data, FUN = 平均)$pred_probs
calibration_plot <- ggplot(calibration_summary, aes(x = pred_mean, y = status)) + geom_line(color = "steelblue", size = 1.2) + geom_point(color = "red", size = 3) + geom_abline(intercept = 0, slope = 1, linetype = "破線", color = "黒", size = 0.8) + labs(title = "ニューラルネットワークの検量線", x = "予測確率", y = "実際の確率") + theme_minimal() + theme(panel.border = element_rect(color = "黒", fill = NA, size = 1))
nn_var_importance <- varImp(nn_model)
importance_df <- data.frame(Feature = rownames(nn_var_importance), 重要度 = nn_var_importance$Overall )
importance_plot <- ggplot(importance_df, aes(x = reorder(Feature, Importance), y = Importance)) + geom_bar(stat = "identity", fill = "steelblue") + coord_flip() + labs(title = "ニューラルネットワークの変数重要度", x = "特徴", y = "重要度") + theme_minimal()
3. 競合リスクモデルの開発・検証
- 次のコードを使用して、単変量解析を実行し、累積罹患率関数 (CIF) 曲線をプロットします。data.csvは、SEERデータベースから取得したデータです。後続の画像を保存する方法は、この手順と同じです。コード内の Site を 1 つずつ他のファクターに置き換えて、すべてのファクターに対して単変量解析を実行します。
図書館(tidycmprsk)
ライブラリ(gtsummary)
ライブラリ(ggplot2)
図書室(ggsurvfit)
図書館(GGPRISM)
AA <- read.csv(「data.csv」)
cif2 <- tidycmprsk::cuminc(Surv(time, Status1) ~Site, data = aa)
tidy(cif2,times = c(12,24,36,48,60))
tbl_cuminc(cif2, times =c(12,24,36,48,60), outcomes = c("CSS", "OSS"),estimate_fun = NULL, label_header = "**{time/12}-year cuminc**") %>%
add_p() %>%
add_n(location = "レベル")
cuminc_plot <- ggcuminc(cif2, outcome = c("CSS", "OSS"), size = 1.5) + labs(x = "time") +add_quantile(y_value = 0.20, size = 1) + scale_x_continuous(breaks = seq(0, 84, by = 12), limits = c(0, 84)) +scale_y_continuous(label = scales::p ercent, breaks = seq(0, 1, by = 0.2), limits = c(0, 1)) + theme_prism() + theme(legend.position = c(0.2, 0.8), panel.grid = element_blank(),panel.grid.major.y = element_line(color = "grey80")) + theme(legend.spacing.x = unit(0.1, "cm"), legend.spacing.y = unit(0.01, "cm")) + theme(axis.ticks.length.x = unit(-0.2, "cm"), axis.ticks.x = element_line(color = "black", size = 1, lineend = 1)) + theme(axis.ticks.length.y = unit(-0.2, "cm"), axis.ticks.y = element_line(color = "black", size = 1, lineend = 1)) - 次のコードを使用して、多変量解析と視覚化を実行します。data1.csvは、前のコードの結果から取得されます。コードを実行した後、[ エクスポート]をクリックし、[ PDFとして保存]をクリックし、最後に[ 保存] をクリックして画像を保存します。
図書館(tidycmprsk)
ライブラリ(gtsummary)
aa <-read.csv('data1.csv')
for (i in names(aa)[c(1:16, 19)]){aa[,i] <- as.factor(aa[,i])}
mul1表2 <- mul1 %>%
gtsummary::tbl_regression(指数 = TRUE) %>%
add_n(location = "レベル");テーブル 2
table_df <- as_tibble(表2)
タブ<-テーブル2$table_body
タブ1 <- タブ[,C(12,19,20,22:29)] - 次のコードを使用して、ノモグラム、ROC曲線、および検量線をプロットします。トレーニング コホートのデータを使用してモデルをトレーニングした後、検証コホートと外部検証コホートのデータを使用して model.library(QHScrnomo) を検証します。外部コホートデータは、ステップ1.4で選択した環状細胞がん以外の結腸直腸がんのサンプルで構成されています。
図書館(RMS)
図書館(timeROC)
図書館(サバイバル)
aa <-read.csv('data3.csv')
for (i in names(aa)[c(1:16, 19)]){aa[,i] <- as.factor(aa[,i])}
DD <- データディスト(AA)
options(datadist = "dd")
mul <- cph(Surv(time, Status1 == 1) ~ T + N + M + LODDS + Site, data = aa, x = TRUE, y = TRUE, surv = TRUE)
M3 <- crr.fit(mul, failcode = 1, cencode = 0)
nomo <-Newlabels(fit = m3, labels =c(T="T", N= "N", M = "M", LODDS = "LODDS", Site = "Site"))
nomoc("N0","N1","N2"),M=c("M0","M1"),LODDS=c
("LODDS1","LODDS2","LODDS3"),サイト=
c("RSC","LSC","直腸")))
nomogram.crr(fit =nomo , lp = F, xfrac = 0.3, fun.at =seq(from=0, to=1, by= 0.1) , failtime =c(12,36,60), funlabel = c("1-year CSS Cumulative Incidence","3-year CSS Cumulative Incidence","5-year CSS Cumulative Incidence"))
time_points <-C(12, 36, 60)
pred_risks_list <- lapply(time_points, function(time_point) {predict(m3, newdata = aa, type = "risk", time = time_point)})
pred_risks_df <- data.frame(do.call(cbind, pred_risks_list))
colnames(pred_risks_df) <- paste("risk_at", time_points, "months", sep = "_")
roc_1year <- timeROC(T = aa$time, delta = ifelse(aa$Status1 == "CSS", 1, 0), marker = pred_risks_df$risk_at_12_months, cause = 1, times = 12, iid = TRUE)
roc_3year <- timeROC(T = aa$time, delta = ifelse(aa$Status1 == "CSS", 1, 0), marker = pred_risks_df$risk_at_36_months, cause = 1, times = 36, iid = TRUE)
roc_5year <- timeROC(T = aa$time, delta = ifelse(aa$Status1 == "CSS", 1, 0), marker = pred_risks_df$risk_at_60_months, cause = 1,times = 60, iid = TRUE)
legend("bottomright",legend = c("1 年間の CSS", "3 年間の CSS", "5 年間の CSS"), col = c("#BF1D2D", "#262626", "#397FC7"), lwd = 2)
sas.cmprsk(m3,時間 = 36)
セットシード(123)
aa$pro <- tenf.crr(m3,時間 = 36)
cindex(prob = aa$pro, fstatus = aa$Status1, ftime = aa$time, type = "crr", failcode = 1, cencode = 0, tol = 1e-20)
groupci(x=aa$pro, ftime = aa$time, fstatus = aa$Status1, failcode = 1, cencode = 0, ci = TRUE, g = 5, m = 1000, u = 36, xlab = "予測確率", ylab = "実際の確率", lty=1, lwd=2, col="#262626",xlim=c(0,1.0), add =TRUE)
結果
患者の特性
この研究は、2004 年から 2015 年までの SEER データベースのデータを使用して、結腸直腸 SRCC と診断された患者に焦点を当てました。除外基準は、生存期間が1ヵ月未満の患者、臨床病理学的情報が不完全な患者、死因が不明または特定されていない症例であった。選択基準を満たした合計2409人の結腸直腸SRCC患者が、トレーニングコホート(N = 1686)と検証コホート(N = 723)にランダムに分けられました。トレーニングコホートとバリデーションコホートの人口統計学的および臨床的パラメータは、 表1に示すようにRソフトウェアを使用して分析されました。対象となった患者のうち、60歳以上が大半を占め、男性患者と女性患者数は同数でした。ほとんどの患者は白人でした。患者の半数以上(56%)が既婚者でした。腫瘍の大部分はIII-IVと等級付けされました(76%)。ほとんどの患者(82%)は腫瘍の大きさが3.5センチメートルを超えており、患者の大多数(42%)はLODDS1グループに属していました。全コホートで、高い割合の患者(53%)が化学療法を受けました。原発腫瘍は主に右結腸に存在していた(67%)。無作為化後、統計的に2つのグループ間でベースライン特性に有意差はありませんでした。
MLモデルに含まれる予後臨床因子の特定
まず、Cox回帰分析を使用して、機械学習モデルに含める有意な変数をスクリーニングしました。単変量Cox回帰の結果は、生存時間が特定の臨床変数、例えば性別、年齢、人種、婚姻状況、AJCC病期分類、pT病期分類、pN病期分類、pM病期分類、腫瘍サイズ、CEAレベル、LNR分類、LODDS分類、および患者が放射線療法または化学療法を受けたかどうかなどの特定の臨床変数と有意に相関していることが示された(表2).特に、LNR、LODDS、およびpN病期分類はすべて統計的に有意なハザード比(HR)を示し、これら3つのLN病期分類システムが予後と関連していることを示しています。その後の多変量Cox回帰分析を実施して、SRCC患者におけるpN病期分類、LODDS、LNR、およびCSS間の関連をさらに決定しました。その結果、SRCC患者のCSSには、LODDS、LNR、およびpNの状態が有意に影響することが示されました(図2)。
LNシステムの比較
3つのLNシステムの予測予後能力は、トレーニング、検証、および外部検証コホート(ステップ1.4で選択された環状細胞がん以外の結腸直腸がんのサンプル)の両方で類似していました。 表3)。トレーニングコホートでは、LNR、LODDS、およびpNのCインデックスはそれぞれ0.309、0.308、および0.337でしたが、検証コホートでは、Cインデックスはそれぞれ0.288、0.279、および0.319でした。外部検証コホートでは、LNR、LODDS、およびpNのCインデックスは、それぞれ0.419、0.420、および0.424でした。さらに、トレーニング コホートの各システムの AIC 値は 12667.56、12670.57、12731.89 であり、検証コホートでは、それぞれ 4575.36、4559.13、4613.20 でした。外部検証コホートでは、各システムのAIC値は、LODDSが106554.68、LNRが106581.85、pN病期分類が106915.45でした。これらの知見は、3つのシステム間での識別品質にわずかな差しかないことを示している。そこで、RF、XGBoost、NNなどの機械学習手法を活用し、予測能力の観点から最適なLNシステムをさらに決定しました。この分析には、単変量Cox回帰で有意な変数と、機械学習モデルを構築するための少なくとも1つの多変量モデル(pN、pT、pM、年齢、人種、LNR分類、LODDS分類、患者が放射線療法を受けたか化学療法を受けたかなど)が含まれていました。
トレーニングデータセットを使用して、RF、XGBoost、およびNNモデルを構築しました。各変数の重要度の値を 図 3 に示します。RFとXGBoostでは、LNRが最も重要性を示し、LODDSもかなりの重要性を示しました。しかし、NNモデルでは、LODDSはpNやLNRと比較して優れた予測能力を示しました。3つの機械学習アプローチを組み合わせた結果を考慮すると、LODDSシステムはSRCC患者のLNステータスを評価するのに最適なシステムであると結論付けています。
ML モデルのパフォーマンス
表4および図4A-Cに示すように、3つのモデルはすべて予後を効果的に予測することができ、テストデータセットでは3つのモデルのAUCは0.777から0.851の範囲でした(XGBoost:AUC = 0.820、95%CI = 0.789-0.851;RF:AUC = 0.819、95%CI = 0.788-0.850;NN: AUC = 0.809, 95% CI = 0.777-0.841)。XGBoost、RF、および NN モデルは、高い特異度 (0.82、0.825、0.815) と精度 (0.762、0.763、0.757) を示しました。検量線を図5D-Fに示します。
競争リスクモデルの構築と検証
MLモデルでは競合するリスク要因の影響が考慮されていなかったため、競合するリスクモデルを構築して、予測能力の点で最も優れたパフォーマンスを発揮するLNシステムをさらに特定しました。がん特異的生存期間(CSS)はがんによる死亡を表し、全生存期間(OSS)は他の原因による死亡を説明し、競合するリスクイベントとして機能します。単変量および多変量競合リスクモデルを使用して、トレーニングコホートにおけるCSSの予測因子を分析しました。単変量競合リスクモデルでは、CSSの予測因子には性別、年齢、人種、婚姻状況、AJCC病期分類、TNM病期分類、腫瘍サイズ、LNR分類、LODDS分類、CEAレベル、患者が放射線療法を受けたか化学療法を受けたか、および原発腫瘍の位置が含まれていたことが示された。最後に、多変量競合リスク解析、T型分類、N型分類、M型分類、LODDS分類、および原発腫瘍の位置が、結腸直腸SRCC患者の5つの独立した予後マーカーとして同定された。単変量および多変量競合リスク分析の結果を 表5に示し、独立したリスク因子に対応する累積発生率関数(CIF)曲線を 図5に示します。5つの有意変数(T病期分類、N病期分類、M病期分類、LODDS分類、および原発腫瘍の位置)に基づいて、予後ノモグラムを作成した(図6A)。その結果、pNと比較して、LODDSはより高いウェイトを示すことがわかりました。この知見は、これまでの結果と一致しており、LODDSシステムがSRCC患者のLNステータスを評価するのに最適なシステムであることを示唆しています。
モデルの精度を評価するために、検量線を作成しました(図6B-D)。その結果、このモデルは、1年、3年、および5年での患者の全生存期間の予測において良好に機能したことが示されました。曲線を45°のラインにフィットさせることで、モデルの強い一貫性が示されています。ノモグラムのROC曲線評価結果(図5E-G)は、1年、3年、5年後の予測の曲線下面積(AUC)が0.75より大きいことを示しました。これらの結果は、3年と5年の予測曲線が有意な利益を示したことを示唆しており、ノモグラムが貴重な臨床応用と参照値を持っていることを示しています。

図1:SEERデータベースでのスクリーニングプロセスを示すフロー図。 私たちの包含基準と除外基準を通じて、私たちは成功裏にRに基づく分析のその後のシリーズのためにSEERデータベースから結腸直腸癌患者を選択しました 。

図2:トレーニングコホートにおけるLNR、LODDS、およびpN病期分類とCSSとの関連。 この図は、(A)LNR、(B)LODDS、および(C)pN病期分類の多変量Cox回帰分析結果を、他の独立した予後因子とともに評価したものです。分析には、ハザード比(HR)と95%信頼区間(CI)が含まれます。この結果は、LNR、LODDS、およびpNの状態が、SRCC患者におけるがん特異的生存の有意な予後因子であり、すべてのHR値が統計的有意性(p < 0.05)を示していることを示している。*p < 0.05、**p < 0.01、***p < 0.001。エラーバーは95%CIを表します。 この図の拡大版を表示するには、ここをクリックしてください。

図3:変数の相対的な重要度(A) XGBoostモデル、 (B) RFモデル、 (C) NNモデル。この図は、変数の相対的な重要度を評価します。XGBoost モデルと RF モデルでは、LNR が最も重要性を示し、LODDS もかなりの重要性を示しました。一方、NNモデルでは、LODDSはpNやLNRと比較して優れた予測能力を示しました。3 つのモデルを組み合わせた結果に基づいて、LODDS システムは SRCC 患者の LN 状態を評価するのに最も効果的であることが示唆されています。 この図の拡大版を表示するには、ここをクリックしてください。

図4:MLモデル、XGBoost、およびeXtremeグラディエントブースティングのROC曲線と検量線。 (A、D)トレーニングコホート、(B、E)検証コホート、(C、F)外部検証コホート。曲線下面積 (AUC) の値が 1 に近いほど、モデルの分類パフォーマンスが優れていることを示します。エラーバーは、実際の事象が発生する予測確率の95%信頼区間を表します。 この図の拡大版を表示するには、ここをクリックしてください。
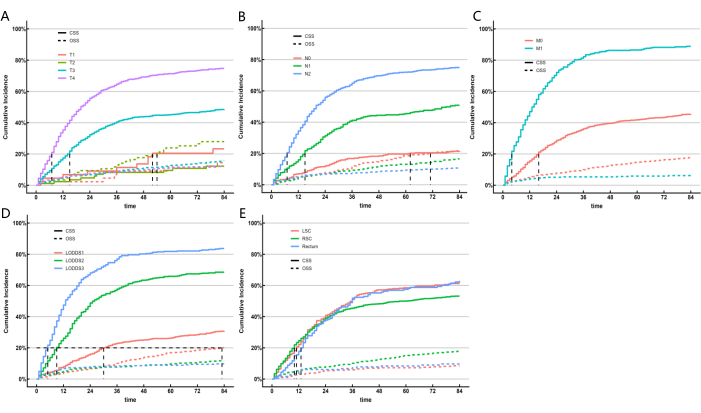
図5:結腸直腸SRCCの患者の特性に応じた死亡の累積発生率推定値。 サブグループの CIF。グレイのテストが適用されました。 この図の拡大版を表示するには、ここをクリックしてください。
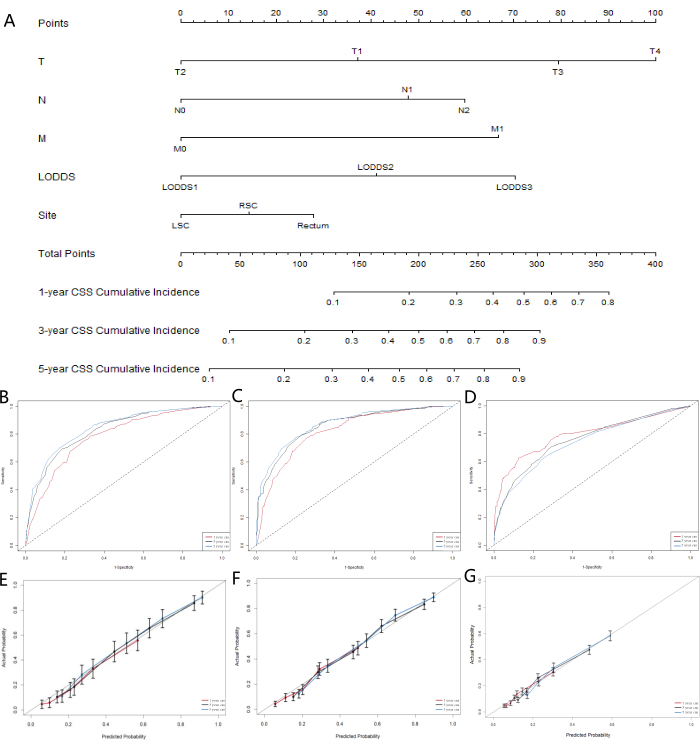
図6:結腸直腸SRCC患者におけるCSSのノモグラムの開発と検証(A)結腸直腸SRCC患者の1年、3年、および5年のがん特異的生存確率を予測する競合リスクノモグラム。(B)トレーニングコホート、(C)検証コホート、および(D)外部検証コホートにおける1年、3年、5年のがん特異的生存を予測するためのノモグラムの検量線。(E) トレーニング コホート、(F) 検証コホート、および (G) 外部検証コホートにおける 1 年、3 年、および 5 年のがん特異的生存を予測するための受信者操作特性曲線。この図の拡大版を表示するには、ここをクリックしてください。
表1:結腸直腸SRCC患者の臨床的特徴。この表をダウンロードするには、ここをクリックしてください。
表2:トレーニングコホートにおけるCSSの単変量Cox回帰分析。この表をダウンロードするには、ここをクリックしてください。
表3:3つのリンパ節の病期分類システムの予測性能。この表をダウンロードするには、ここをクリックしてください。
表4:検証コホートと外部検証コホートのモデルの予測性能。この表をダウンロードするには、ここをクリックしてください。
表5:トレーニングコホートにおける結腸直腸SRCCのがん特異的死亡率に関する単変量および多変量競合リスク分析。この表をダウンロードするには、ここをクリックしてください。
ディスカッション
結腸直腸癌(CRC)SRCCは、予後不良の結腸直腸癌のまれで特別なサブタイプです。したがって、SRCC患者の予後には、より一層の注意を払う必要があります。SRCC患者の正確な生存予測は、患者の予後を判断し、個別の治療決定を下すために重要です。本研究では、SRCC患者における臨床的特徴と予後との関連を検討し、SEERデータベースからSRCC患者に最適なLN病期分類システムを特定した。私たちの知る限り、これは、機械学習と競合するリスク分析方法を包括的に使用して結腸直腸SRCC患者に適したLNシステムを決定し、予後予測のためのノモグラムを構築するための最初の研究です。
CRC患者における転移性LNの数は、予後と再発の重要な指標です。正確なLN病期分類は、SRCC患者の治療戦略と予後を決定する上で重要な役割を果たします。LNRおよびLODDSは、GCへのLNの関与を評価し、病期分類システムを改善し、より正確な予後情報を提供するために使用される代替方法である10,13。SRCC患者におけるLODDS、LNR、およびpN病期分類とCSSとの相関関係をSEERデータベースを用いて明らかにした。これら3つのLNシステム(LNR、LODDS、PN)の予測能力を、AUC、AIC、BIC、Cインデックスを用いて比較しました。しかし、それらの違いはごくわずかでした。そこで、Xgboost、RF、NNの3つの機械学習手法を用いて、最適なLNシステムとして最も重要な特徴を選定しました。3つの方法を組み合わせた結果に基づいて、LODDSを適切なLNシステムとして定義しました。
ただし、OSS は CSS 患者の予後に影響を与える競合するリスク イベントです。Cox回帰法を使用して機械学習モデルに含める変数をスクリーニングするプロセスでは、OSSの影響が考慮されていなかったため、リスク比の評価が不正確になる可能性があります12。そこで、SRCC患者に最適なLN評価システムをさらに決定するために、競合するリスクモデルを構築しました。その結果、LODDS病期分類システムは、pNシステムと比較してより正確な予後情報を提供することが改めて確認されました。追跡期間中、2409人の患者のうち、1339人(56%)がCSSで死亡し、464人(19%)がOSSで死亡しました。さらに、1年、3年、5年でのがん特異的死亡率を予測するための競合リスクチャートも作成した。このモデルは、結腸直腸SRCC患者を対象とした臨床研究に大きな意味を持つと考えています。米国がん合同委員会は、すべての組織型大腸がんの病期分類システムとしてTNMシステムを推奨していますが、主に結腸直腸腺がんの病期分類に使用されます。AJCC NステージはTLNによって制限されていますが、LNRはNLN13,14,15,16の影響を考慮していません。レポートによると、LODDS は TLN の影響をあまり受けず、NLN10,17 の数を考慮しています。Scarinciらは、LODDSがLNRおよびpN病期分類よりもCRC患者のOSをよりよく予測することを示し、将来の研究ではさまざまなCRCサブタイプにおけるその役割を検証する必要があることを示唆しました18。この研究では、LODDSが結腸直腸SRCCのCSSに有意な予後予測効果をもたらすことがわかりました。したがって、LODDS は、結腸直腸 SRCC 患者のリンパ節郭清と予後を評価するための貴重なツールになる可能性があります。LODDSの最適なしきい値はまだ確立されていませんが、最も信頼性の高いLNステージングシステムであることが証明されています。LODDSへの注目が高まるにつれ、近い将来、臨床現場で広く認知されるようになると一般に考えられています。
私たちの研究では、原発腫瘍の位置が CSS の重要な予測因子であり、直腸 SRCC の予後が著しく不良であることがわかり、これは以前の研究と一致しています 12,19,20。直腸SRCCは、独自の臨床的、病理学的、および分子的特徴を有する可能性があり21,22、さらなる研究が必要である。予測モデルから導き出されたチャートは、臨床上の意思決定と患者カウンセリングのための重要かつ効果的なツールです。私たちの知る限り、この研究は、ML モデルと競合するリスク モデルを統合して、SRCC 患者に最適な LN 病期分類システムを探求した最初の研究です。SRCC患者の予後を予測するために、3つのMLモデルを開発し、検証しました。テストデータセットでは、XGBoost、RF、および NN モデルは、AUC 値と対応するメトリクスに基づいて、良好な予後予測パフォーマンスを示しました。したがって、ML モデルは、予後を予測することにより、SRCC 患者の治療決定を支援できます。さらに、比例ハザードモデルに基づいて競合するリスクチャートを作成し、結腸直腸SRCCの予測因子を分析し、その中でのLODDSの役割を評価しました。Cインデックスと検量線を使用して、ノモグラムの予測性能を評価しました。このチャートには、腫瘍の原発部位やLODDSのグループ化など、一般的な臨床変数が表示されていました。さらに、本研究で構築したノモグラムは、大腸SRCC患者における1年、3年、5年のCSSを予測する有効な方法である。このツールは、臨床医が各結腸直腸SRCC患者に対して正確で徹底的かつタイムリーな予後評価を行うのを支援し、彼らが個別の治療計画を策定することを可能にします23。
最後に、この研究にはいくつかの制限があります。まず、この研究に参加した患者は2004年から2015年の間に診断されたため、追跡期間は比較的短かった。追跡期間を長くすることで、モデル予測の精度が向上すると期待しています。第二に、ここで使用される研究デザインは遡及的であり、SEERデータベースから取得したデータに依存しているため、いくつかの固有のバイアスが生じる可能性があります。転移性LNの位置など、一部の情報は記録されませんでした。最後に、この研究の患者の大多数は白人であったため、これらの知見を確認し強化するためには、多様な集団を対象とした広範な研究が必要でした。
結論
この研究では、LODDSが結腸直腸SRCCの強力な予後予測能力を示すことがわかりました。この基盤に基づいて、結腸直腸SRCC患者の1年、3年、および5年間隔での全生存率を予測するための競合リスクモデルに基づくノモグラムを開発しました。一連の評価と内部検証の結果、ノモグラムは臨床への適用性と価値が高く評価され、臨床医が治療の意思決定を行う際のガイダンスとなっています。さらに、3つのMLモデルを構築しました。これらのMLアプローチは、SRCCの予後予測機能を強化し、医師がMLをどのように活用して治療とフォローアップ戦略を最適化できるかを理解するのに役立つ可能性を秘めています。
開示事項
著者には、開示すべき金銭的な利益相反はありません。
謝辞
何一つ
資料
| Name | Company | Catalog Number | Comments |
| SEER database | National Cancer institiute at NIH | ||
| X-tile software | Yale school of medicine | ||
| R-studio | Posit |
参考文献
- Siegel, R. L., Giaquinto, A. N., Jemal, A. Cancer statistics, 2024. CA Cancer J Clin. 74 (1), 12-49 (2024).
- Korphaisarn, K., et al. Signet ring cell colorectal cancer: Genomic insights into a rare subpopulation of colorectal adenocarcinoma. Br J Cancer. 121 (6), 505-510 (2019).
- Willauer, A. N., et al. Clinical and molecular characterization of early-onset colorectal cancer. Cancer. 125 (12), 2002-2010 (2019).
- Watanabe, A., et al. A case of primary colonic signet ring cell carcinoma in a young man which preoperatively mimicked Phlebosclerotic colitis. Acta Med Okayama. 73 (4), 361-365 (2019).
- Kim, H., Kim, B. H., Lee, D., Shin, E. Genomic alterations in signet ring and mucinous patterned colorectal carcinoma. Pathol Res Pract. 215 (10), 152566(2019).
- Deng, X., et al. Neoadjuvant radiotherapy versus surgery alone for stage II/III mid-low rectal cancer with or without high-risk factors: A prospective multicenter stratified randomized trial. Ann Surg. 272 (6), 1060-1069 (2020).
- Buk Cardoso, L., et al. Machine learning for predicting survival of colorectal cancer patients. Sci Rep. 13 (1), 8874(2023).
- Monterrubio-Gómez, K., Constantine-Cooke, N., Vallejos, C. A. A review on statistical and machine learning competing risks methods. Biom J. 66 (2), e2300060(2024).
- Kim, H. J., Choi, G. S. Clinical implications of lymph node metastasis in colorectal cancer: Current status and future perspectives. Ann Coloproctol. 35 (3), 109-117 (2019).
- Xu, T., et al. Log odds of positive lymph nodes is an excellent prognostic factor for patients with rectal cancer after neoadjuvant chemoradiotherapy. Ann Transl Med. 9 (8), 637(2021).
- Chen, Y. R., et al. Prognostic performance of different lymph node classification systems in young gastric cancer. J Gastrointest Oncol. 12 (4), 285-1300 (2021).
- Bouvier, A. M., et al. How many nodes must be examined to accurately stage gastric carcinomas? Results from a population based study. Cancer. 94 (11), 2862-2866 (2002).
- Coburn, N. G., Swallow, C. J., Kiss, A., Law, C. Significant regional variation in adequacy of lymph node assessment and survival in gastric cancer. Cancer. 107 (9), 2143-2151 (2006).
- Li Destri, G., Di Carlo, I., Scilletta, R., Scilletta, B., Puleo, S. Colorectal cancer and lymph nodes: the obsession with the number 12. World J Gastroenterol. 20 (8), 1951-1960 (2014).
- Dinaux, A. M., et al. Outcomes of persistent lymph node involvement after neoadjuvant therapy for stage III rectal cancer. Surgery. 163 (4), 784-788 (2018).
- Sun, Y., Zhang, Y., Huang, Z., Chi, P. Prognostic implication of negative lymph node count in ypN+ rectal cancer after neoadjuvant chemoradiotherapy and construction of a prediction nomogram. J Gastrointest Surg. 23 (5), 1006-1014 (2019).
- Xu, Z., Jing, J., Ma, G. Development and validation of prognostic nomogram based on log odds of positive lymph nodes for patients with gastric signet ring cell carcinoma. Chin J Cancer Res. 32 (6), 778-793 (2020).
- Scarinci, A., et al. The impact of log odds of positive lymph nodes (LODDS) in colon and rectal cancer patient stratification: a single-center analysis of 323 patients. Updates Surg. 70 (1), 23-31 (2018).
- Nitsche, U., et al. Prognosis of mucinous and signet-ring cell colorectal cancer in a population-based cohort. J Cancer Res Clin Oncol. 142 (11), 2357-2366 (2016).
- Kang, H., O'Connell, J. B., Maggard, M. A., Sack, J., Ko, C. Y. A 10-year outcomes evaluation of mucinous and signet-ring cell carcinoma of the colon and rectum. Dis Colon Rectum. 48 (6), 1161-1168 (2005).
- Sung, C. O., et al. Clinical significance of signet ring cells in colorectal mucinous adenocarcinoma. Mod Pathol. 21 (12), 1533-1541 (2008).
- Alvi, M. A., et al. Molecular profiling of signet ring cell colorectal cancer provides a strong rationale for genomic targeted and immune checkpoint inhibitor therapies. Br J Cancer. 117 (2), 203-209 (2017).
- Brownlee, S., et al. Evidence for overuse of medical services around the world. Lancet. 390 (10090), 156-168 (2017).
転載および許可
このJoVE論文のテキスト又は図を再利用するための許可を申請します
許可を申請さらに記事を探す
This article has been published
Video Coming Soon
Copyright © 2023 MyJoVE Corporation. All rights reserved