Method Article
Comparación del rendimiento predictivo de tres sistemas de estadificación de ganglios linfáticos en el carcinoma colorrectal de células en anillo con sello basado en un modelo de aprendizaje automático
* Estos autores han contribuido por igual
En este artículo
Resumen
Este estudio evalúa los sistemas pronósticos para pacientes con carcinoma colorrectal de células en anillo de sello utilizando modelos de aprendizaje automático y análisis de riesgo competitivos. Identifica las probabilidades logarítmicas de ganglios linfáticos positivos como un predictor superior en comparación con la estadificación de pN, lo que demuestra un sólido rendimiento predictivo y ayuda a la toma de decisiones clínicas a través de sólidas herramientas de predicción de supervivencia.
Resumen
El estado de los ganglios linfáticos es un predictor pronóstico crítico para los pacientes; sin embargo, el pronóstico del carcinoma colorrectal de células en anillo de sello (SRCC, por sus siglas en inglés) ha recibido poca atención. Este estudio investiga la capacidad predictiva pronóstica de las probabilidades logarítmicas de ganglios linfáticos positivos (LODDS), la proporción de ganglios linfáticos (LNR) y la estadificación de pN en pacientes con SRCC utilizando modelos de aprendizaje automático (Random Forest, XGBoost y Neural Network) junto con modelos de riesgo competitivos. Los datos relevantes se extrajeron de la base de datos Surveillance, Epidemiology, and End Results (SEER). Para los modelos de aprendizaje automático, se identificaron factores pronósticos para la supervivencia específica del cáncer (CSS) a través de análisis de regresión de Cox univariados y multivariados, seguidos de la aplicación de tres métodos de aprendizaje automático (XGBoost, RF y NN) para determinar el sistema óptimo de estadificación de los ganglios linfáticos. En el modelo de riesgo competitivo, se emplearon análisis de riesgo competitivos univariados y multivariados para identificar factores pronósticos, y se construyó un nomograma para predecir el pronóstico de los pacientes con SRCC. Se utilizaron el área bajo la curva de características de operación del receptor (AUC-ROC) y las curvas de calibración para evaluar el rendimiento del modelo. Un total de 2.409 pacientes con SRCC fueron incluidos en este estudio. Para validar la efectividad del modelo, se incluyó una cohorte adicional de 15.122 pacientes con cáncer colorrectal, excluyendo los casos de SRCC, para su validación externa. Tanto los modelos de aprendizaje automático como el nomograma de riesgo de la competencia mostraron un sólido rendimiento en la predicción de los resultados de supervivencia. En comparación con la estadificación de pN, los sistemas de estadificación LODDS demostraron una capacidad pronóstica superior. Tras la evaluación, los modelos de aprendizaje automático y los modelos de riesgo de la competencia lograron un excelente rendimiento predictivo caracterizado por una buena discriminación, calibración e interpretabilidad. Nuestros hallazgos pueden ayudar a informar la toma de decisiones clínicas para los pacientes.
Introducción
El cáncer colorrectal (CCR) se sitúa como el tercer tumor maligno más prevalente a nivel mundial 1,2,3. El carcinoma de células en anillo de sello (CCR), un subtipo raro de CCR, comprende aproximadamente el 1% de los casos y se caracteriza por abundante mucina intracelular que desplaza el núcleo celular 1,2,4. El SRCC a menudo se asocia con pacientes más jóvenes, tiene una prevalencia más alta en mujeres y tiene estadios tumorales avanzados en el momento del diagnóstico. En comparación con el adenocarcinoma colorrectal, el SRCC muestra una peor diferenciación, un mayor riesgo de metástasis a distancia y una tasa de supervivencia a 5 años de solo 12-20%5,6. El desarrollo de un modelo pronóstico preciso y eficaz para el SRCC es crucial para optimizar las estrategias de tratamiento y mejorar los resultados clínicos.
Este estudio tiene como objetivo construir un modelo pronóstico sólido para pacientes con SRCC utilizando enfoques estadísticos avanzados, incluido el aprendizaje automático (ML) y modelos de riesgo competitivos. Estas metodologías pueden acomodar relaciones complejas en los datos clínicos, ofreciendo evaluaciones de riesgo individualizadas y superando a los métodos tradicionales en precisión predictiva. Los modelos de aprendizaje automático, como Random Forest, XGBoost y Neural Networks, sobresalen en el procesamiento de datos de alta dimensión y la identificación de patrones intrincados. Los estudios han demostrado que los modelos de IA predicen eficazmente los resultados de supervivencia en el cáncer colorrectal, lo que enfatiza el potencial del ML en aplicaciones clínicas 7,8. Como complemento al ML, los modelos de riesgo que compiten entre sí abordan múltiples tipos de eventos, como la mortalidad específica del cáncer frente a otras causas de muerte, para refinar el análisis de supervivencia. A diferencia de los métodos tradicionales como el estimador de Kaplan-Meier, los modelos de riesgo competitivos estiman con precisión la probabilidad marginal de eventos en presencia de riesgos contrapuestos, proporcionando evaluaciones de supervivencia más precisas8. La integración del ML y el análisis de riesgos de la competencia mejora el rendimiento predictivo, ofreciendo un marco potente para herramientas de pronóstico personalizadas en SRCC 9,10,11.
La metástasis ganglionar influye significativamente en el pronóstico y la recidiva en los pacientes con CCR. Si bien la evaluación de la etapa N en la clasificación TNM es crítica, el examen inadecuado de los ganglios linfáticos, reportado en el 48% al 63% de los casos, puede llevar a una subestimación de la enfermedad. Para abordar esto, se han introducido enfoques alternativos como la proporción de ganglios linfáticos (LNR) y las probabilidades logarítmicas de ganglios linfáticos positivos (LODDS). La LNR, la proporción de ganglios linfáticos positivos (PLN) con respecto al total de ganglios linfáticos (TLN), se ve menos afectada por el recuento de TLN y sirve como factor pronóstico en el CCR. La LODDS, la relación logarítmica de PLNs a ganglios linfáticos negativos (NLNs), ha mostrado una capacidad predictiva superior tanto en el SRCC gástrico como en el cáncer colorrectal10,11. El aprendizaje automático se ha aplicado cada vez más en oncología, con modelos que mejoran la estratificación del riesgo y las predicciones pronósticas en varios tipos de cáncer, incluidos los cánceres de mama, próstata y pulmón 12,13,14. Sin embargo, su aplicación en el SRCC colorrectal sigue siendo limitada.
Este estudio busca cerrar esta brecha mediante la integración de LODDS con ML y modelos de riesgo competitivos para crear una herramienta de pronóstico integral. Mediante la evaluación del valor pronóstico de LODDS y el aprovechamiento de técnicas predictivas avanzadas, esta investigación tiene como objetivo mejorar la toma de decisiones clínicas y mejorar los resultados para los pacientes con SRCC.
Protocolo
Este estudio no se refiere a la aprobación ética y el consentimiento para participar. Los datos utilizados en este estudio se obtuvieron de bases de datos. Incluimos pacientes diagnosticados con carcinoma colorrectal de células en anillo de sello entre 2004 y 2015, así como otros tipos de cáncer colorrectal. Los criterios de exclusión incluyeron pacientes con un tiempo de supervivencia menor de un mes, aquellos con información clinicopatológica incompleta y casos en los que la causa de la muerte no estaba clara o no se especificó.
1. Adquisición de datos
- Descargar SEER. Obtener estadísticas 8.4.3 software del sitio web de la base de datos SEER (http://seer.cancer.gov/about/overview.html). Después de iniciar sesión en el software, haga clic en Sesión de lista de casos > Datos y seleccionar la base de datos Incidence SEER Research Plus Data, 17 Registros, Nov 2021 Sub (2000-2019).
- Haga clic en Selección > Editar y elija {Raza, Sexo, Año Dx. Año de diagnóstico} = '2004', '2005', '2006', '2007', '2008', '2009', '2010', '2011', '2012', '2013', '2014', '2015' Y {Sitio y Morfología. Recodificación del sitio ICD-O-3/OMS 2008} = '8490/3'.
- A continuación, haga clic en Tabla y, en la interfaz de variables disponibles, seleccione Recodificación por edad con edades únicas y 100+, Sexo, Matrimonio, Recodificación del sitio ICD-O-3/OMS 2008, Tamaño del tumor CS, Regional nodes_examined(1988+), Regional nodes_positive(1988+), Derivado AJCC Stage Group, 6ª ed. (2004-2015), Derivado AJCC T, 6ª ed. (2004-2015), Derivado AJCC N, 6ª ed. (2004-2015), Derivado AJCC M, 6ª ed. (2004-2015), CEA, Recodificación de la radiación, Recodificación de la quimioterapia (sí, no/unk), Clasificación de la muerte por causa específica del SEER, Recodificación del estado vital (se utiliza el límite del estudio), Meses de supervivencia, Año del diagnóstico.
- Finalmente, haga clic en Salida, asigne un nombre a los datos y haga clic en Ejecutar para generar y guardar los datos. El proceso de inclusión detallado se muestra en la Figura 1.
- Descargue los datos de los pacientes con cáncer colorrectal, excluyendo los casos de SRCC, para su posterior validación externa. Haga clic en Selección > Editar y elija {Raza, Sexo, Año Dx. Año de diagnóstico} = '2004', '2005', '2006', '2007', '2008', '2009', '2010', '2011', '2012', '2013', '2014', '2015' Y {Sitio principal - etiquetado} = 'C18-C20'. Repita los pasos 1.3 y 1.4 para obtener información clínico patológica y excluir muestras con {Sitio y morfología. Recodificación del sitio ICD-O-3/WHO 2008} = '8490/3' del archivo descargado.
- Con fines comparativos, procese varias variables. Clasifique el estado de los ganglios linfáticos utilizando la proporción de ganglios linfáticos (LNR) y el logaritmo de las probabilidades de ganglios linfáticos positivos (LODDS).
- Defina la LNR como la proporción de ganglios linfáticos positivos (PLN) con respecto al total de ganglios linfáticos (TLN). Calcule el valor de LODDS utilizando la fórmula:
loge(número de PLN + 0,5) / (número de ganglios linfáticos negativos (NLN) + 0,5)
donde se agregó 0.5 para evitar un resultado infinito. Los valores de corte para LNR, LODDS y tamaño tumoral se determinaron mediante el software X-tile (versión 3.6.1) basado en el método del valor P mínimo.
- Defina la LNR como la proporción de ganglios linfáticos positivos (PLN) con respecto al total de ganglios linfáticos (TLN). Calcule el valor de LODDS utilizando la fórmula:
- Abra el software X-tile, haga clic en Archivo > Abrir y seleccione el archivo de datos para importarlo al software. Una vez cargados los datos, mapee las variables: Censor corresponde al estado de supervivencia, Tiempo de supervivencia corresponde al tiempo de supervivencia y Marcador1 es la variable a analizar, asegurándose de que los datos coincidan correctamente.
- A continuación, haga clic en Hacer > marcador de > de Kaplan-Meier1 para realizar el análisis de supervivencia de Kaplan-Meier y generar la curva de supervivencia. Sobre la base de la separación de las curvas de supervivencia de Kaplan-Meier, la significación estadística (p. ej., valor p) y la relevancia clínica, determine el valor de corte óptimo y, finalmente, registre o exporte los resultados del análisis.
- Divida el LNR en tres grupos: LNR 1 (≤0,16), LNR 2 (0,16 - 0,78) y LNR 3 (≥ 0,78). Clasifique a los pacientes en tres grupos según LODDS: LODDS 1 (≤ -1,44), LODDS 2 (-1,44 - 0,86) y LODDS 3 (≥ 0,86).
- Clasifique el tamaño del tumor en tres categorías: ≤ 3,5 cm, 3,5 - 5,5 cm y ≥ 5,5 cm. Convierta la edad de una variable continua a una variable categórica. Clasifique las edades de los pacientes en el momento del diagnóstico inicial como ≥60 años y <60 años. Clasifique la ubicación del tumor según la distribución de los tumores de carcinoma de células en anillo de sello (SRCC) como colon derecho, colon izquierdo y recto. El colon derecho incluye el ciego, el colon ascendente, la flexura hepática y el colon transverso, mientras que el colon izquierdo incluye la flexión esplénica, el colon descendente, el colon sigmoide y la unión rectosigmoidea.
- Para este estudio, asigne aleatoriamente un total de 2409 datos de pacientes elegibles con SRCC a una cohorte de entrenamiento (N = 1686) y una cohorte de validación (N = 723) en una proporción de 7:3. Utilice el siguiente código para la división aleatoria y obtenga data.csv de la base de datos SEER. Los archivos generados después de la división aleatoria se utilizarán para un análisis posterior.
Biblioteca(intercalación)
<- read.csv("data.csv")
set.semilla(123)
train_indices <- createDataPartition(data$variable, p = 0.7, list = FALSE)
train_data <- datos[train_indices, ]
test_data <- datos[-train_indices, ]
write.csv(train_data, "traindata.csv", row.names = FALSE)
write.csv(test_data, "testdata.csv", row.names = FALSE)
2. Desarrollo y verificación de modelos de ML
- Descargue el software RStudio (2024.04.2+764) y R (4.4.1). Abra RStudio para ejecutar el software de R. Haga clic en Nuevo archivo y seleccione R Script para crear una nueva interfaz de programación de R. Introduzca el código correspondiente en el editor de código y haga clic en Ejecutar para ejecutar el código.
- Utilice el siguiente código para filtrar las variables incluidas en los modelos de ML mediante el análisis de regresión de Cox. Además, explore el impacto de la estadificación de LODDS, LNR y pN en la supervivencia específica del cáncer (CSS) en pacientes con SRCC. El traindata.csv son los datos obtenidos de la base de datos SEER.
biblioteca("supervivencia")
Biblioteca("survminer")
biblioteca("rms")
biblioteca("dplyr")
<- read.csv("traindata.csv")
data$time=as.numeric(data$time)
data$status=as.numeric(data$status)
variables <- c("Sexo", "Edad", "Raza", "Matrimonio", "Etapa", "T", "N", "M","Tumor_size", "LNR", "LODDS", "CEA", "Radiación", "Quimioterapia", "Sitio")
datos <- datos %>%
mutar(a través(all_of(variables), as.factor))
cox=coxph(Surv(tiempo, estado) ~ datos$T, datos = datos)
Coeficientes de Cox$
pval=anova(cox)$Pr[2]
clean_data=datos[,c(1:12, 14:18)]
get_coxVariable=función(your_data,índice){cox_list=c() k=1
for (i in 1:index) {mod=coxph(Surv(time, status) ~ your_data[,i],data=your_data) pval=anova(mod)$Pr[2] print(pval) print(colnames(your_data)[i]) if (pval<0.05) {cox_list[k]=colnames(your_data)[i] k=k+1}}return(cox_list)}
variable_select=get_coxVariable(clean_data,15)
for(i en 1:15){print(variable_select[i])}
for (var in variable_select) {formula <- as.formula(paste("Surv(time, status) ~", var))cox_model <- coxph(formula, data = data) print(summary(cox_model))
ggforest(timonel)
variables <- c("Sexo", "Edad", "Raza", "Matrimonio", "Estadio", "T", "N", "M", "Tumor_size", "LNR", "LODDS", "Quimioterapia")
datos <- datos %>%
mutar(a través(all_of(variables), as.factor))
cox=coxph(Surv(tiempo, estado) ~ Sexo + Edad + Raza + Matrimonio + T + N + M + Tumor_size + LNR +
LODDS+Quimioterapia, datos = datos)
ggforest(cox,datos = datos)
ggplot_forest <- ggforest(cox, datos = datos) - Utilice el siguiente código para comparar las capacidades de predicción pronóstica de tres sistemas LN (LODDS, LNR y estadificación pN) en las cohortes de entrenamiento, validación y validación externa.
Biblioteca (RMS)
Biblioteca(Supervivencia)
Biblioteca(Survminer)
biblioteca(riskRegression)
Biblioteca(gt)
train_data <- read.csv("train_data123.csv")
validation_data <- read.csv("test_data123.csv")
dd <- datadist(train_data)
opciones(datadist = "dd")
model_LNR <- cph(Surv(tiempo, estado) ~ LNR, datos = train_data, x = VERDADERO, y = VERDADERO)
model_LODDS <- cph(Surv(tiempo, estado) ~ LODDS, datos = train_data, x = VERDADERO, y = VERDADERO)
model_pN <- cph(Surv(tiempo, estado) ~ N, datos = train_data, x = VERDADERO, y = VERDADERO)
calculate_performance <- function(modelo, datos) {pred <- predict(modelo, newdata = datos) c_index_result <- concordancia(Surv(data$time, data$status) ~ pred) c_index <- c_index_result$concordancia aic <- AIC(modelo) bic <- BIC(modelo) return(c(C_index = round(c_index, 3), AIC = round(aic, 2), BIC = round(bic, 2)))}
calculate_performance <- function(modelo, datos) {pred <- predict(model, newdata = datos, type = "lp") concordance_result <- concordancefit(Surv(data$time, data$status), x = pred) c_index <- concordance_result$concordancia ci_lower <- c_index - 1.96 * sqrt(concordance_result$var) ci_upper <- c_index + 1.96 * sqrt(concordance_result$var) aic <- AIC(modelo) bic <- BIC(modelo) return(c(C_Index = round(c_index, 3), CI_Lower = redondo(ci_lower, 3), CI_Upper = redondo(ci_upper, 3), AIC = redondo(aic, 2), BIC = redondo(bic, 2)))}
train_LNR <- calculate_performance(model_LNR train_data)
train_LODDS <- calculate_performance(model_LODDS train_data)
train_pN <- calculate_performance(model_pN train_data)
model_LNR_val <- cph(Surv(tiempo, estado) ~ LNR, datos = validation_data, x = VERDADERO, y = VERDADERO)
model_LODDS_val <- cph(Surv(tiempo, estado) ~ LODDS, datos = validation_data, x = VERDADERO, y = VERDADERO)
model_pN_val <- cph(Surv(tiempo, estado) ~ N, datos = validation_data, x = VERDADERO, y = VERDADERO)
val_LNR <- calculate_performance(model_LNR_val validation_data)
val_LODDS <- calculate_performance(model_LODDS_val validation_data)
val_pN <- calculate_performance(model_pN_val validation_data)
resultados <- data.frame(Variable = c("LNR", "LODDS", "pN"), Training_C_Index = c(paste(train_LNR["C_Index"], "(", train_LNR["CI_Lower"], ", ", train_LNR["CI_Upper"], ")", sep = ""), paste(train_LODDS["C_Index"], "(", train_LODDS["CI_Lower"], ", train_LODDS["CI_Upper"], ")", sep = ""), paste(train_pN["C_Index"], "(", train_pN["CI_Lower"], ", ", train_pN["CI_Upper"], ")", sep = "")), Training_AIC = c(train_LNR["AIC"], train_LODDS["AIC"], train_pN["AIC"]), Training_BIC = c(train_LNR["BIC"], train_LODDS["BIC"], train_pN["BIC"]), Validation_C_Index = c(pegar(val_LNR["C_Index"], "(", val_LNR["CI_Lower"], ", val_LNR["CI_Upper"], ")", sep = ""), paste(val_LODDS["C_Index"], "(", val_LODDS["CI_Lower"], ", ", val_LODDS["CI_Upper"], ")", sep = ""), paste(val_pN["C_Index"], "(", val_pN["CI_Lower"], ", ", val_pN["CI_Upper"], ")", sep = "")), Validation_AIC = c(val_LNR["AIC"], val_LODDS["AIC"], val_pN["AIC"]), Validation_BIC = c(val_LNR["BIC"], val_LODDS["BIC"], val_pN["BIC"]))
results_table <- gt(resultados) %>%
tab_header(title = "Rendimiento de predicción de los tres sistemas de estadificación de los ganglios linfáticos") %>%
cols_label(Variable = "Variable",Training_C_Index = "Índice C (IC del 95%) (Formación)", Training_AIC = "AIC (Formación)", Training_BIC = "BIC (Formación)", Validation_C_Index = "Índice C (IC del 95%) (Validación)", Validation_AIC = "AIC (Validación)", Validation_BIC = "BIC (Validación)")
write.csv(resultados, "prediction_performance.csv", fila.nombres = FALSO) - Utilice el siguiente código para crear un modelo XGBoost y generar gráficos de barras de la importancia relativa de las variables, para comparar así la importancia de los tres sistemas LN. Del mismo modo, genere curvas ROC y curvas de calibración. Los datos se obtienen de la base de datos SEER.
Biblioteca(xgboost)
Biblioteca(intercalación)
biblioteca (pROC)
train_data <- read.csv("train_data.csv")
test_data <- read.csv("test_data.csv")
train_matrix <- XGB. DMatrix(data = as.matrix(train_data[, c('Edad', 'T', 'N', 'M', 'LODDS', 'Quimioterapia')]), label = train_data$status)
test_matrix <- XGB. DMatrix(data = as.matrix(test_data[, c('Edad', 'T', 'N', 'M', 'LODDS', 'Quimioterapia')]), label = test_data$status)
params <- list(booster = "gbtree", objective = "binary:logistic", eval_metric = "auc", eta = 0.1, max_depth = 6, subsample = 0.8, colsample_bytree = 0.8)
xgb_model <- xgb.train(params = params, data = train_matrix, nrounds = 100, watchlist= list(train = train_matrix), verbose = 1)
pred_probs <- predict(xgb_model, newdata = test_matrix)
pred_labels <- ifelse(pred_probs > 0.5, 1, 0)
conf_matrix <- confusionMatrix(as.factor(pred_labels), as.factor(test_data$status))
roc_curve <- roc(test_data$status, pred_probs)
auc_value <- auc(roc_curve)
ci_auc <- ci.auc(roc_curve)
sensibilidad <- conf_matrix$byClass["Sensibilidad"]
specificidad <- conf_matrix$byClass["Especificidad"]
precisión <- conf_matrix$overall["Precisión"]
ppv <- conf_matrix$byClass["Pos Pred Value"]
npv <- conf_matrix$byClass["Valor de Neg Pred"]
result_table <- data.frame(Modelo = "XGBoost", AUC = sprintf("%.3f (%.3f-%.3f)", auc_value, ci_auc[1], ci_auc[3]), Sensibilidad = sprintf("%.3f", sensibilidad), Especificidad = sprintf("%.3f", especificidad), Precisión = sprintf("%.3f", precisión), PPV = sprintf("%.3f", ppv), NPV = sprintf("%.3f", npv))
write.csv(result_table, "xgboost_model_performance.csv", row.names = FALSE)
roc_df <- data.frame(FPR = 1 - roc_curve$especificidades, TPR = roc_curve$sensibilidades)
roc_plot <- ggplot(roc_df, aes(x = FPR, y = TPR)) +geom_line(color = "steelblue", tamaño = 1.2) + geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "gris") + annotate("text", x = 0.9, y = 0.2, label = paste("AUC =", round(auc_value, 3)), size = 5, color = "black") + labs(title = "ROC Curve for XGBoost Model", x = "Tasa de falsos positivos", y = "Tasa de verdaderos positivos") + theme_minimal() + theme(panel.border = element_rect(color = "negro", relleno = NA, tamaño = 1))
calibration_data <- data.frame(Status = as.factor(test_data$status), pred_probs = pred_probs)
calib_model <- calibración (Estado ~ pred_probs, datos = calibration_data, clase = "1", cortes = 5)
ggplot(calib_model$data, aes(x = punto medio, y = porcentaje)) + geom_line(color = "steelblue", tamaño = 1) + geom_point(color = "rojo", tamaño = 2) + geom_abline(intersección = 0, pendiente = 1, tipo de línea = "discontinuo", color = "negro") +labs(título = "Curva de calibración para el modelo XGBoost", x = "Probabilidad predicha", y = "proporción observada") + theme_minimal() + theme(panel.border = element_rect(color = "negro", relleno = NA, tamaño = 0.5)) - Utilice el siguiente código para construir un modelo de RF y generar gráficos de barras de la importancia relativa de las variables, comparando así la importancia de los tres sistemas LN. Del mismo modo, genere curvas ROC y curvas de calibración. Los datos se obtienen de la base de datos SEER.library(randomForest)
Biblioteca(dplyr)
biblioteca(ggplot2)
biblioteca (pROC)
Biblioteca(intercalación)
Biblioteca (RMS)
tren <- read.csv("train_data.csv")
Probado <- read.csv("test_data.csv")
trainset$status=factor(trainset$status)
variables1 <- c("Edad", "T", "N", "M", "LODDS", "Quimioterapia")
Tren <- Tren %>%
mutar(a través(all_of(variables1), as.numérico))
testsed$status=factor(testsed$status)
Probado <- Probado %>%
mutar(a través(all_of(variables1), as.numérico))
RF=randomForest(trainset$status ~ Edad + T + N + M + LODDS + Quimioterapia, data=trainset,ntree=100,importance=TRUE,proximity=TRUE)
imp=importancia(RF)
varImpPlot(RF)
impvar=rownames(imp)[order(imp[,4],decreciente = VERDADERO)]
importance_df <- as.data.frame(imp)
importance_df$Variables <- rownames(importance_df)
importance_plot <- ggplot(importance_df, aes(x = reorder(Variables, MeanDecreaseAccuracy), y = MeanDecreaseAccuracy)) +geom_bar(stat = "identity", fill = "steelblue") +coord_flip() + labs(title = "Importancia de la variable", x = "Variables", y = "Precisión de la disminución media") + theme_minimal()
pred_probs <- predict(RF, testset, type = "prob")[,2]
roc_obj <- roc(testset$status, pred_probs)
auc_value <- auc(roc_obj)
roc_plot <- ggplot() +geom_line(aes(x = 1 - roc_obj$especificidades, y = roc_obj$sensibilidades), color = "steelblue", tamaño = 1.2) +geom_abline(intersección = 0, pendiente = 1, tipo de línea = "discontinuo", color = "gris") + anotar ("texto", x = 0.8, y = 0.2, etiqueta = pegar("AUC =", redondo(auc_value, 3)), color = "negro", tamaño = 5, hjust = 0) + labs(título = "Curva ROC para modelo de bosque aleatorio", x = "Tasa de falsos positivos", y = "Tasa de verdaderos positivos") +theme_minimal() + theme(panel.border = element_rect(color = "negro", relleno = NA, tamaño = 1))
calibration_data <- data.frame(pred_probs = pred_probs, status = testsed$status)
calib_model <- calibración (estado ~ pred_probs, datos = calibration_data, clase = "1", cortes = 5)
calib_df <- as.data.frame(calib_model[["datos"]])
calib_df$ medio <- calib_df$punto medio
calib_df$Porcentaje <- calib_df$Porcentaje
calibration_plot <- ggplot(calib_df, aes(x = mid, y = Porcentaje)) + geom_line(color = "steelblue", tamaño = 1.2) + geom_point(color = "steelblue", tamaño = 3) + geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "black", size = 0.8) + labs(title = "Curva de calibración para bosque aleatorio", x = "Probabilidad predicha", y = "Probabilidad real") + theme_minimal() + theme(panel.border = element_rect(color = "negro", fill = NA, tamaño = 1), plot.title = element_text(hjust = -0.05, vjust = -1.5, face = "bold", size = 12) )
rf_probs <- predict(RF, newdata=testsed, type="prob")[, 2]
rf_auc <- roc(testsed$status, rf_probs)
auc_value <- auc(rf_auc)
ci_auc <- ci.auc(rf_auc)
rf_predictions <- predict(RF, newdata=probado)
conf_matrix <- confusionMatrix(rf_predictions, testsed$status)
sensibilidad <- conf_matrix$byClass["Sensibilidad"]
specificidad <- conf_matrix$byClass["Especificidad"]
precisión <- conf_matrix$overall["Precisión"]
ppv <- conf_matrix$byClass["Pos Pred Value"]
npv <- conf_matrix$byClass["Valor de Neg Pred"]
result_table <- data.frame(Modelo = "RF", AUC = sprintf("%.3f (%.3f-%.3f)", auc_value, ci_auc[1], ci_auc[3]), Sensibilidad = sprintf("%.3f", sensibilidad), Especificidad = sprintf("%.3f", especificidad), Precisión = sprintf("%.3f", precisión), PPV = sprintf("%.3f", ppv), NPV = sprintf("%.3f", npv))
write.csv(result_table, "RF_model_performance.csv", row.names = FALSE) - Utilice el siguiente código para crear un modelo NN y generar gráficos de barras de la importancia relativa de las variables, comparando así la importancia de los tres sistemas LN. Del mismo modo, genere curvas ROC y curvas de calibración. Los datos se obtienen de la base de datos SEER.library(nnet)
Biblioteca(intercalación)
biblioteca (pROC)
biblioteca(ggplot2)
train_data <- read.csv("train_data.csv")
test_data <- read.csv("test_data.csv")
train_data$status <- as.factor(train_data$status)
test_data$status <- as.factor(test_data$status)
características <- c ("Edad", "T", "N", "M", "LODDS", "Quimioterapia")
x_train <- train_data[, características]
y_train <- train_data$estado
x_test <- test_data[, características]
y_test <- test_data$status
nn_model <- nnet(estado ~ Edad + T + N + M + LODDS + Quimioterapia, datos = train_data, tamaño = 5, caries = 0,01, máx. = 200)
pred_probs <- predict(nn_model, newdata = x_test, type = "raw")
pred_labels <- ifelse(pred_probs > 0.5, 1, 0)
roc_curve <- roc(as.numeric(y_test), pred_probs)
auc_value <- auc(roc_curve)
auc_ci <- ci.auc(roc_curve)
auc_text <- paste0(round(auc_value, 3), " (", round(auc_ci[1], 3), "-", round(auc_ci[3], 3), ")")
conf_matrix <- confusionMatrix(as.factor(pred_labels), y_test)
precisión <- conf_matrix$overall["Precisión"]
sensibilidad <- conf_matrix$byClass["Sensibilidad"]
specificidad <- conf_matrix$byClass["Especificidad"]
ppv <- conf_matrix$byClass["Pos Pred Value"]
npv <- conf_matrix$byClass["Valor de Neg Pred"]
performance_table <- data.frame(Métrica = c("AUC (IC 95%)", "Precisión", "Sensibilidad", "Especificidad", "PPV", "NPV"),Valor = c(auc_text, redondo(precisión, 3), redondo(sensibilidad, 3), redondo(especificidad, 3), redondo(ppv, 3), redondo(npv, 3)))
write.csv(performance_table, "NN_performance_table.csv", row.names = FALSE)
roc_curve <- roc(y_test, pred_probs)
auc_value <- auc(roc_curve)
roc_plot <- ggplot() + geom_line(aes(x = 1 - roc_curve$especificidades, y = roc_curve$sensibilidades), color = "steelblue", tamaño = 1.2) +geom_abline(intersección = 0, pendiente = 1, tipo de línea = "discontinuo", color = "gris") + anotar ("texto", x = 0.8, y = 0.2, etiqueta = pegar("AUC =", redondo(auc_value, 3)), color = "negro", tamaño = 5, hjust = 0) + labs(título = "Curva ROC para modelo de red neuronal", x = "Tasa de falsos positivos", y = "Tasa de verdaderos positivos") + theme_minimal() + theme(panel.border = element_rect(color = "negro", relleno = NA, tamaño = 1))
calibration_data <- data.frame(pred_probs = pred_probs, status = as.numeric(y_test) - 1)
calibration_data$pred_probs <- as.numeric(calibration_data$pred_probs)
calibration_data$calibration_bin <- corte(calibration_data$pred_probs, breaks = seq(0, 1, by = 0.2), include.lowest = TRUE)
calibration_summary <- agregado(estado ~ calibration_bin, datos = calibration_data, DIVERSIÓN = media)
calibration_summary$pred_mean <- agregado(pred_probs ~ calibration_bin, datos = calibration_data, DIVERSIÓN = media)$pred_probs
calibration_plot <- ggplot(calibration_summary, aes(x = pred_mean, y = estado)) + geom_line(color = "steelblue", tamaño = 1.2) + geom_point(color = "rojo", tamaño = 3) + geom_abline(intersección = 0, pendiente = 1, tipo de línea = "discontinuo", color = "negro", tamaño = 0.8) + labs(título = "Curva de calibración para red neuronal", x = "Probabilidad predicha", y = "Probabilidad real") + theme_minimal() + theme(panel.border = element_rect(color = "negro", relleno = NA, tamaño = 1))
nn_var_importance <- varImp(nn_model)
importance_df <- data.frame(Característica = nombres de fila(nn_var_importance), Importancia = nn_var_importance$Overall )
importance_plot <- ggplot(importance_df, aes(x = reorder(Característica, Importancia), y = Importancia)) + geom_bar(stat = "identidad", fill = "steelblue") + coord_flip() + labs(title = "Importancia variable para la red neuronal", x = "Características", y = "Importancia") + theme_minimal()
3. Desarrollo y verificación de modelos de riesgo competitivos
- Utilice el siguiente código para realizar un análisis univariante y trazar la curva de la función de incidencia acumulada (CIF). El data.csv son los datos obtenidos de la base de datos SEER. El método para guardar las imágenes posteriores será el mismo que en este paso. Reemplace el sitio en el código uno por uno con otros factores para realizar un análisis univariante para todos los factores.
Biblioteca(tidycmprsk)
biblioteca(gtresumen)
biblioteca(ggplot2)
Biblioteca(ggsurvfit)
Biblioteca(ggprisma)
aa <- read.csv("data.csv")
cif2 <- tidycmprsk::cuminc(Surv(time, Status1) ~Site, data = aa)
tidy(cif2,veces = c(12,24,36,48,60))
tbl_cuminc(cif2, times =c(12,24,36,48,60), outcomes = c("CSS", "OSS"),estimate_fun = NULL, label_header = "**{time/12}-year cuminc**") %>%
add_p() %>%
add_n(ubicación = "nivel")
cuminc_plot <- ggcuminc(cif2, resultado = c("CSS", "OSS"), tamaño = 1.5) + labs(x = "tiempo") +add_quantile(y_value = 0.20, tamaño = 1) + scale_x_continuous(breaks = seq(0, 84, by = 12), limits = c(0, 84)) +scale_y_continuous(label = scales::p ercent, breaks = seq(0, 1, by = 0.2), limits = c(0, 1)) + theme_prism() + theme(legend.position = c(0.2, 0.8), panel.grid = element_blank(),panel.grid.major.y = element_line(color = "grey80")) + theme(legend.spacing.x = unit(0.1, "cm"), legend.spacing.y = unit(0.01, "cm")) + theme(axis.ticks.length.x = unit(-0.2, "cm"), axis.ticks.x = element_line(color = "negro", tamaño = 1, lineend = 1)) + theme(axis.ticks.length.y = unit(-0.2, "cm"), axis.ticks.y = element_line(color = "negro", tamaño = 1, lineend = 1)) - Utilice el siguiente código para realizar análisis y visualización multivariante. El data1.csv proviene de los resultados del código anterior. Después de ejecutar el código, haga clic en Exportar, luego haga clic en Guardar como PDF y finalmente haga clic en Guardar para guardar la imagen.
Biblioteca(tidycmprsk)
biblioteca(gtresumen)
AA <-read.csv(«data1.csv»)
for (i in names(aa)[c(1:16, 19)]){aa[,i] <- as.factor(aa[,i])}
mul1Tabla2 <- MUL1 %>%
gtsummary::tbl_regression(exponenciado = VERDADERO) %>%
add_n(ubicación = "nivel"); Tabla 2
table_df <- as_tibble(tabla 2)
Pestaña <- Mesa2$table_body
tab1 <- tab[,c(12,19,20,22:29)] - Utilice el siguiente código para trazar el nomograma, la curva ROC y la curva de calibración. Después de entrenar el modelo con datos de la cohorte de entrenamiento, use los datos de las cohortes de validación y validación externa para validar el model.library(QHScrnomo). Los datos de cohorte externa consisten en muestras de cáncer colorrectal distinto del carcinoma de células anular, que se seleccionaron en el paso 1.4.
Biblioteca (RMS)
biblioteca(timeROC)
Biblioteca(Supervivencia)
AA <-read.csv(«data3.csv»)
for (i in names(aa)[c(1:16, 19)]){aa[,i] <- as.factor(aa[,i])}
dd <- datadist(aa)
opciones(datadist = "dd")
mul <- cph(Surv(tiempo, Estado1 == 1) ~ T + N + M + LODDS + Sitio, datos = aa, x = VERDADERO, y = VERDADERO, surv = VERDADERO)
M3 <- CRR.fit(MUL, failcode = 1, cencode = 0)
nomo <-Newlabels(fit = m3, labels =c(T="T", N= "N", M = "M", LODDS = "LODDS", Site = "Site"))
nomoc("N0","N1","N2"),M=c("M0","M1"),LODDS=c
("LODDS1","LODDS2","LODDS3"),Sitio=
c("RSC","LSC","Recto")))
nomogram.crr(fit =nomo , lp = F, xfrac = 0.3, fun.at =seq(from=0, to=1, by= 0.1) , failtime =c(12,36,60), funlabel = c("Incidencia acumulativa de CSS de 1 año","Incidencia acumulativa de CSS de 3 años","Incidencia acumulativa de CSS de 5 años"))
time_points <- C(12, 36, 60)
pred_risks_list <- lapply(time_points, function(time_point) {predict(m3, newdata = aa, type = "risk", time = time_point)})
pred_risks_df <- data.frame(do.call(cbind, pred_risks_list))
colnames(pred_risks_df) <- pegar("risk_at", time_points, "meses", sep = "_")
roc_1year <- timeROC(T = aa$time, delta = ifelse(aa$Status1 == "CSS", 1, 0), marker = pred_risks_df$risk_at_12_months, cause = 1, times = 12, iid = TRUE)
roc_3year <- timeROC(T = aa$time, delta = ifelse(aa$Status1 == "CSS", 1, 0), marker = pred_risks_df$risk_at_36_months, cause = 1, times = 36, iid = TRUE)
roc_5year <- timeROC(T = aa$time, delta = ifelse(aa$Status1 == "CSS", 1, 0), marker = pred_risks_df$risk_at_60_months, cause = 1,times = 60, iid = TRUE)
legend("abajo a la derecha",legend = c("CSS de 1 año", "CSS de 3 años", "CSS de 5 años"), col = c("#BF1D2D", "#262626", "#397FC7"), lwd = 2)
sas.cmprsk(m3,tiempo = 36)
set.semilla(123)
aa$pro <- tenf.crr(m3,tiempo = 36)
cindex(prob = aa$pro, fstatus = aa$Status1, ftime = aa$time, type = "crr", failcode = 1, cencode = 0, tol = 1e-20)
groupci(x=aa$pro, ftime = aa$time, fstatus = aa$Status1, failcode = 1, cencode = 0, ci = TRUE, g = 5, m = 1000, u = 36, xlab = "Probabilidad predicha", ylab = "Probabilidad real", lty=1, lwd=2, col="#262626",xlim=c(0,1.0), ylim=c(0,1.0), add =TRUE)
Resultados
Características de los pacientes
Este estudio se centró en pacientes diagnosticados con SRCC colorrectal, utilizando datos de la base de datos SEER que abarcan desde 2004 hasta 2015. Los criterios de exclusión incluyeron pacientes con un tiempo de supervivencia menor de un mes, aquellos con información clinicopatológica incompleta y casos en los que la causa de la muerte no estaba clara o no se especificó. Un total de 2409 pacientes con SRCC colorrectal que cumplieron con los criterios de inclusión se dividieron aleatoriamente en una cohorte de entrenamiento (N = 1686) y una cohorte de validación (N = 723). Los parámetros demográficos y clínicos de las cohortes de entrenamiento y validación se analizaron mediante el software R, como se muestra en la Tabla 1. Entre todos los pacientes incluidos, la mayoría tenía más de 60 años, con un número similar de pacientes masculinos y femeninos. La mayoría de los pacientes eran blancos. Más de la mitad de los pacientes (56%) estaban casados. La mayoría de los tumores se clasificaron como III-IV (76 %). La mayoría de los pacientes (82 %) tenían tumores de más de 3,5 cm, y la mayoría de los pacientes pertenecían al grupo LODDS1 (42 %). En toda la cohorte, una alta proporción de pacientes (53%) recibió quimioterapia. Los tumores primarios se localizaron principalmente en el colon derecho (67%). Después de la aleatorización, no hubo diferencias significativas en las características basales entre los dos grupos desde el punto de vista estadístico.
Identificación de los factores clínicos pronósticos incluidos en los modelos de ML
En primer lugar, seleccionamos las variables significativas para incluirlas en el modelo de aprendizaje automático mediante el análisis de regresión de Cox. Los resultados de la regresión univariada de Cox mostraron que el tiempo de supervivencia se correlacionó significativamente con ciertas variables clínicas, como el sexo, la edad, la raza, el estado civil, la estadificación del AJCC, la estadificación pT, la estadificación del pN, la estadificación del pM, el tamaño del tumor, el nivel de CEA, la clasificación de LNR, la clasificación de LODDS y si el paciente recibió radioterapia o quimioterapia (Tabla 2). En particular, la estadificación de LNR, LODDS y pN exhibió cocientes de riesgos instantáneos (CRI) estadísticamente significativos, lo que indica que estos tres sistemas de estadificación de LN se relacionan con el pronóstico. Posteriormente, se llevó a cabo un análisis de regresión multivariante de Cox para determinar la asociación entre la estadificación de pN, LODDS, LNR y CSS en pacientes con SRCC. Los resultados indicaron que el estado de LODDS, LNR y pN afectó significativamente el CSS de los pacientes con SRCC (Figura 2).
Comparación de sistemas LN
Las capacidades pronósticas predictivas de los tres sistemas de LN fueron similares en las cohortes de entrenamiento, validación y validación externa (muestras de cáncer colorrectal distinto del carcinoma de células anular, que se seleccionaron en el paso 1.4; Tabla 3). En la cohorte de formación, los índices C para LNR, LODDS y pN fueron de 0,309, 0,308 y 0,337, respectivamente, mientras que en la cohorte de validación, los índices C fueron de 0,288, 0,279 y 0,319, respectivamente. En la cohorte de validación externa, los índices C para LNR, LODDS y pN fueron 0,419, 0,420 y 0,424, respectivamente. Además, los valores de AIC para cada sistema en la cohorte de entrenamiento fueron 12667.56, 12670.57 y 12731.89, y en la cohorte de validación, fueron 4575.36, 4559.13 y 4613.20, respectivamente. En la cohorte de validación externa, los valores de AIC para cada sistema fueron los siguientes: 106554,68 para LODDS, 106581,85 para LNR y 106915,45 para la estadificación de pN. Estos resultados indican que existen diferencias mínimas en la calidad discriminatoria entre los tres sistemas. Por lo tanto, utilizamos métodos de aprendizaje automático (RF, XGBoost y NN) para determinar aún más el sistema LN óptimo en términos de capacidad predictiva. Este análisis incluyó variables que fueron significativas en la regresión univariada de Cox y al menos un modelo multivariado (pN, LODDS o LNR) para la construcción de los modelos de aprendizaje automático, incluyendo pN, pT, pM, edad, raza, clasificación LNR, clasificación LODDS y si el paciente recibió radioterapia o quimioterapia.
Construimos modelos RF, XGBoost y NN utilizando el conjunto de datos de entrenamiento. Los valores de importancia de cada variable se muestran en la Figura 3. En RF y XGBoost, LNR exhibió la mayor importancia, mientras que LODDS también demostró una importancia considerable. Sin embargo, en el modelo NN, LODDS mostró una mejor capacidad predictiva en comparación con pN y LNR. Teniendo en cuenta los resultados combinados de los tres enfoques de aprendizaje automático, concluimos que el sistema LODDS puede ser el mejor sistema para evaluar el estado de LN en pacientes con SRCC.
Rendimiento de los modelos de ML
Como se muestra en la Tabla 4 y en la Figura 4A-C, los tres modelos fueron capaces de predecir el pronóstico de manera efectiva, y los AUC de los tres modelos oscilaron entre 0,777 y 0,851 en el conjunto de datos de prueba (XGBoost: AUC = 0,820, IC del 95% = 0,789-0,851; RF: AUC = 0,819, IC 95% = 0,788-0,850; NN: AUC = 0,809, IC 95% = 0,777-0,841). Los modelos XGBoost, RF y NN mostraron una gran especificidad (0,82, 0,825, 0,815) y precisión (0,762, 0,763, 0,757). Las curvas de calibración se muestran en la Figura 5D-F.
Construcción y validación de modelo de riesgo competitivo
Dado que los modelos de ML no tuvieron en cuenta la influencia de los factores de riesgo contrapuestos, construimos un modelo de riesgo competitivo para identificar aún más el sistema LN que funcionó mejor en términos de capacidad predictiva. La supervivencia específica del cáncer (CSS, por sus siglas en inglés) representa la muerte por cáncer, mientras que la supervivencia general (OSS, por sus siglas en inglés) representa las muertes por otras causas, que sirven como eventos de riesgo que compiten entre sí. Utilizamos modelos de riesgo competitivos univariados y multivariados para analizar los factores predictivos de CSS en la cohorte de entrenamiento. El modelo de riesgo univariado competitivo indicó que los factores predictivos de CSS incluyeron el sexo, la edad, la raza, el estado civil, la estadificación del AJCC, la estadificación TNM, el tamaño del tumor, la clasificación de LNR, la clasificación de LODDS, el nivel de CEA, si el paciente recibió radioterapia o quimioterapia y la ubicación del tumor primario. Por último, se identificaron el análisis de riesgo competitivo multivariante, la estadificación T, la estadificación N, la estadificación M, la clasificación LODDS y la ubicación del tumor primario como cinco marcadores pronósticos independientes para los pacientes con SRCC colorrectal. En la Tabla 5 se muestran los resultados de los análisis de riesgo univariados y multivariados que compiten entre sí, y en la Figura 5 se presentan las curvas de la función de incidencia acumulada (CIF) correspondientes para los factores de riesgo independientes. A partir de las cinco variables significativas (estadificación T, estadificación N, estadificación M, clasificación LODDS y localización del tumor primario), elaboramos un nomograma pronóstico (Figura 6A). Encontramos que, en comparación con pN, LODDS mostró un mayor peso. Este hallazgo se alinea con los resultados anteriores, lo que sugiere que el sistema LODDS es el mejor sistema para evaluar el estado de LN en pacientes con SRCC.
Para evaluar la precisión del modelo, construimos curvas de calibración (Figuras 6B-D). Los resultados indicaron que el modelo funcionó bien en la predicción de la supervivencia total de los pacientes a 1, 3 y 5 años. El ajuste de las curvas a la línea de 45° demuestra una fuerte consistencia del modelo. Los resultados de la evaluación de la curva ROC para el nomograma (Figuras 5E-G) mostraron que el área bajo la curva (AUC) para las predicciones a 1, 3 y 5 años fue mayor que 0,75. Estos resultados sugieren que las curvas de predicción a 3 y 5 años demostraron beneficios significativos, lo que indica que el nomograma tiene valiosas aplicaciones clínicas y valor de referencia.

Figura 1: Diagrama de flujo que presenta el proceso de cribado en la base de datos SEER. A través de nuestros criterios de inclusión y exclusión, seleccionamos con éxito a los pacientes con cáncer colorrectal de la base de datos SEER para una serie posterior de análisis basados en R. Haga clic aquí para ver una versión más grande de esta figura.

Figura 2: Asociación de la estadificación de LNR, LODDS y pN con CSS en la cohorte de entrenamiento. Esta figura ilustra los resultados del análisis de regresión multivariante de Cox para (A) LNR, (B) LODDS y (C) pN estadificación, evaluados junto con otros factores pronósticos independientes. El análisis incluye cocientes de riesgo instantáneo (HR) e intervalos de confianza (IC) del 95%. Los resultados demuestran que el estado de LNR, LODDS y pN son factores pronósticos significativos para la supervivencia específica del cáncer en pacientes con SRCC, y todos los valores de HR muestran significación estadística (p < 0,05). *p < 0,05, **p < 0,01, ***p < 0,001. Las barras de error representan un IC del 95%. Haga clic aquí para ver una versión más grande de esta figura.

Figura 3: Importancia relativa de las variables. (A) Modelo XGBoost, (B) modelo RF y (C) modelo NN. En esta figura se evalúa la importancia relativa de las variables. En los modelos XGBoost y RF, LNR exhibió la mayor importancia, y LODDS también mostró una importancia considerable. Por el contrario, en el modelo NN, LODDS demostró una capacidad predictiva superior en comparación con pN y LNR. Sobre la base de los resultados combinados de los tres modelos, se sugiere que el sistema LODDS es el más eficaz para evaluar el estado de LN en pacientes con SRCC. Haga clic aquí para ver una versión más grande de esta figura.

Figura 4: Curvas ROC y curvas de calibración de los modelos ML, XGBoost y eXtreme gradient boosting. (A, D) la cohorte de entrenamiento, (B, E) la cohorte de validación y (C, F) la cohorte de validación externa. El valor del área bajo la curva (AUC) más cercano a 1 indica un mejor rendimiento de clasificación del modelo. Las barras de error representan el intervalo de confianza del 95% para la probabilidad predicha de que ocurra el evento real. Haga clic aquí para ver una versión más grande de esta figura.
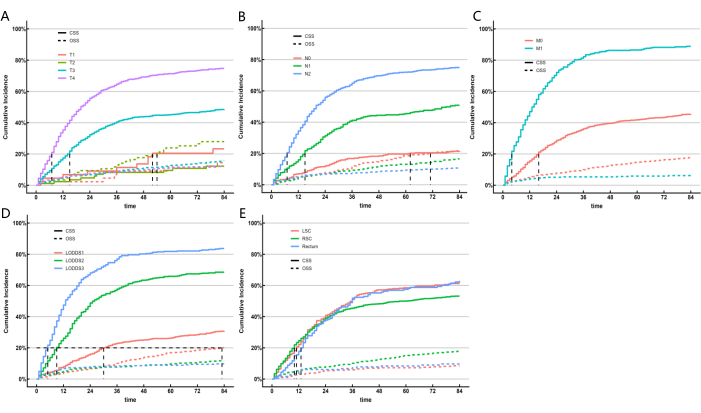
Figura 5: Estimación de la incidencia acumulada de muerte según las características del paciente en el CCRC colorrectal. CIF de subgrupos. Se aplicó la prueba de Gray. Haga clic aquí para ver una versión más grande de esta figura.
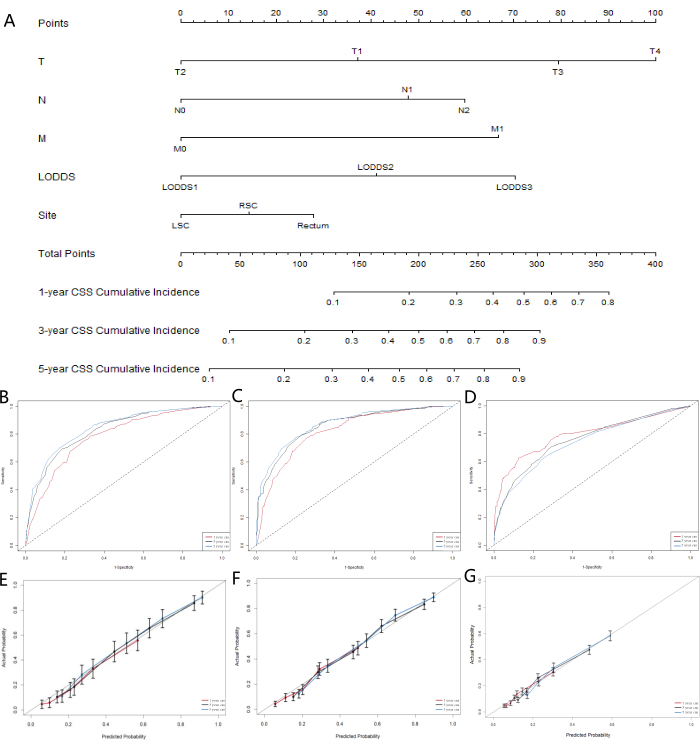
Figura 6: Desarrollo y validación de nomogramas para CSS en pacientes con SRCC colorrectal. (A) Un nomograma de riesgo competitivo que predice la probabilidad de supervivencia específica del cáncer a 1 año, 3 años y 5 años de pacientes con SRCC colorrectal. Las curvas de calibración de los nomogramas para predecir la supervivencia específica del cáncer a 1, 3 y 5 años en la cohorte de entrenamiento (B), (C) la cohorte de validación y (D) la cohorte de validación externa. Curvas características operativas del receptor para predecir la supervivencia específica del cáncer a 1, 3 y 5 años en la cohorte de entrenamiento (E), la cohorte de validación (F) y la cohorte de validación externa (G). Haga clic aquí para ver una versión más grande de esta figura.
Tabla 1: Características clínicas de los pacientes con CCRC colorrectal. Haga clic aquí para descargar esta tabla.
Tabla 2: Análisis de regresión univariada de Cox de CSS en la cohorte de entrenamiento. Haga clic aquí para descargar esta tabla.
Tabla 3: Rendimiento de la predicción de los tres sistemas de estadificación de los ganglios linfáticos. Haga clic aquí para descargar esta tabla.
Tabla 4: Comportamiento predictivo de los modelos en la cohorte de validación y cohortes de validación externa. Haga clic aquí para descargar esta tabla.
Tabla 5: Análisis de riesgo competitivo univariado y multivariado para la mortalidad específica por cáncer de SRCC colorrectal en la cohorte de entrenamiento. Haga clic aquí para descargar esta tabla.
Discusión
Cáncer colorrectal (CCR) El cáncer colorrectal es un subtipo raro y especial de cáncer colorrectal con un pronóstico precario. Por lo tanto, es necesario prestar mayor atención al pronóstico de los pacientes con SRCC. La predicción precisa de la supervivencia de los pacientes con SRCC es crucial para determinar su pronóstico y tomar decisiones de tratamiento individualizadas. En este estudio, exploramos la relación entre las características clínicas y el pronóstico en pacientes con SRCC e identificamos el sistema óptimo de estadificación de LN para pacientes con SRCC de la base de datos SEER. Hasta donde sabemos, este es el primer estudio que determina el sistema de LN adecuado para los pacientes con SRCC colorrectal mediante un uso integral del aprendizaje automático y los métodos de análisis de riesgos competitivos y para construir un nomograma para la predicción pronóstica.
El número de LN metastásicos en los pacientes con CCR es un indicador importante de pronóstico y recurrencia. La estadificación precisa de la NL desempeña un papel clave en la determinación de las estrategias de tratamiento y el pronóstico de los pacientes con SRCC. La LNR y la LODDS son métodos alternativos utilizados para evaluar la participación de la LN en la GC, mejorar los sistemas de estadificación y proporcionar información pronóstica más precisa10,13. Revelamos la correlación entre la estadificación de LODDS, LNR y pN con CSS en pacientes con SRCC utilizando la base de datos SEER. Las capacidades predictivas de estos tres sistemas LN (LNR, LODDS y pN) se compararon utilizando los índices AUC, AIC, BICI y C. Sin embargo, las diferencias entre ellos eran mínimas. Por lo tanto, utilizamos tres métodos de aprendizaje automático (Xgboost, RF y NN) para seleccionar las características más importantes como el sistema LN óptimo. Sobre la base de los resultados combinados de los tres métodos, definimos LODDS como el sistema LN apropiado.
Sin embargo, el OSS es un evento de riesgo competitivo que afecta el pronóstico de los pacientes con CSS. El proceso de selección de variables para su inclusión en el modelo de aprendizaje automático utilizando el método de regresión de Cox no consideró el impacto de OSS, lo que puede llevar a una evaluación inexacta de los cocientes de riesgo12. Por lo tanto, para determinar aún más el sistema óptimo de evaluación de LN para los pacientes con SRCC, construimos un modelo de riesgo competitivo. Los resultados confirmaron una vez más que el sistema de estadificación LODDS proporciona información pronóstica más precisa en comparación con el sistema pN. Durante el seguimiento, entre 2409 pacientes, 1339 (56%) murieron de CSS y 464 (19%) murieron de OSS. Además, también desarrollamos una tabla de riesgo competitiva para predecir las tasas de mortalidad específicas por cáncer a 1 año, 3 años y 5 años. Creemos que este modelo tiene implicaciones significativas para la investigación clínica con pacientes con SRCC colorrectal. Aunque el American Joint Committee on Cancer recomienda el sistema TNM como sistema de estadificación para todos los tipos histológicos de cáncer colorrectal, se usa principalmente para estadificar el adenocarcinoma colorrectal. La etapa N del AJCC está limitada por TLN, mientras que la LNR no considera el impacto de NLN 13,14,15,16. Los informes indican que LODDS se ve menos afectado por la TLN y considera el número de NLN10,17. Scarinci et al. demostraron que la LODDS predice la SG en los pacientes con CCR mejor que la estadificación de la LNR y la pN y sugirieron que futuras investigaciones deberían validar su papel en diferentes subtipos de CCR18. En este estudio, encontramos que LODDS tiene un efecto pronóstico predictivo significativo sobre el CSS en el SRCC colorrectal. Por lo tanto, la LODDS puede ser una herramienta valiosa para evaluar la disección y el pronóstico de los ganglios linfáticos en pacientes con CCRC colorrectal. Aunque todavía no se ha establecido un umbral óptimo para LODDS, ha demostrado ser el sistema de estadificación de LN más fiable. Con el aumento de la atención a LODDS, se cree generalmente que ganará un amplio reconocimiento en los entornos clínicos en el futuro previsible.
Nuestro estudio encontró que la localización del tumor primario es un factor predictivo importante para el CSS, con un pronóstico significativamente peor para el SRCC rectal, lo que es consistente con estudios previos 12,19,20. El SRCC rectal puede tener características clínicas, patológicas y moleculares únicas 21,22, lo que justifica una mayor investigación. Los gráficos derivados de los modelos predictivos son herramientas clave y efectivas para la toma de decisiones clínicas y el asesoramiento al paciente. Hasta donde sabemos, este estudio es el primero en integrar modelos de ML y modelos de riesgo competitivos para explorar el sistema óptimo de estadificación de LN para pacientes con SRCC. Desarrollamos y validamos tres modelos de ML para predecir el pronóstico de los pacientes con SRCC. En el conjunto de datos de prueba, los modelos XGBoost, RF y NN mostraron un buen rendimiento predictivo pronóstico basado en los valores de AUC y las métricas correspondientes. Por lo tanto, los modelos de ML pueden ayudar en las decisiones de tratamiento para los pacientes con SRCC mediante la predicción del pronóstico. Además, generamos gráficos de riesgo competitivos basados en modelos de riesgo proporcional para analizar los factores predictivos del SRCC colorrectal y evaluar el papel de LODDS dentro de él. Utilizamos el índice C y las curvas de calibración para evaluar el rendimiento predictivo del nomograma. El gráfico mostraba variables clínicas comunes, como el sitio primario del tumor y la agrupación de LODDS. Además, el nomograma que construimos es un método eficaz para predecir el CSS a 1 año, 3 años y 5 años en pacientes con SRCC colorrectal. Esta herramienta puede ayudar a los médicos a realizar evaluaciones pronósticas precisas, exhaustivas y oportunas para cada paciente con SRCC colorrectal, lo que les permite formular planes de tratamiento personalizados23.
Finalmente, este estudio tiene varias limitaciones. En primer lugar, los pacientes del estudio fueron diagnosticados entre 2004 y 2015, lo que llevó a un período de seguimiento relativamente corto. Anticipamos que un período de seguimiento más largo ayudaría a mejorar la precisión de las predicciones de los modelos. En segundo lugar, el diseño del estudio utilizado aquí es retrospectivo y se basa en datos obtenidos de la base de datos SEER, lo que puede introducir algunos sesgos inherentes. No se registró parte de la información, como la ubicación de las LN metastásicas. Por último, la mayoría de los pacientes de este estudio eran blancos, por lo que se necesitan estudios más amplios que involucren a diversas poblaciones para confirmar y reforzar estos hallazgos.
Conclusión
El estudio encontró que el LODDS exhibe una fuerte capacidad predictiva pronóstica para el SRCC colorrectal. Sobre la base de esta base, desarrollamos un nomograma basado en un modelo de riesgo competitivo para predecir las tasas de supervivencia general a intervalos de 1 año, 3 años y 5 años para pacientes con SRCC colorrectal. Después de una serie de evaluaciones y validaciones internas, el nomograma ha demostrado una aplicabilidad y un valor clínicos significativos, proporcionando orientación a los médicos en la toma de decisiones sobre el tratamiento. Además, construimos tres modelos de ML. Estos enfoques de ML tienen el potencial de mejorar las capacidades predictivas de pronóstico para SRCC y ayudar a los médicos a comprender cómo se puede utilizar ML para optimizar el tratamiento y las estrategias de seguimiento.
Divulgaciones
Los autores no tienen conflictos de intereses financieros que revelar.
Agradecimientos
Ninguno
Materiales
| Name | Company | Catalog Number | Comments |
| SEER database | National Cancer institiute at NIH | ||
| X-tile software | Yale school of medicine | ||
| R-studio | Posit |
Referencias
- Siegel, R. L., Giaquinto, A. N., Jemal, A. Cancer statistics, 2024. CA Cancer J Clin. 74 (1), 12-49 (2024).
- Korphaisarn, K., et al. Signet ring cell colorectal cancer: Genomic insights into a rare subpopulation of colorectal adenocarcinoma. Br J Cancer. 121 (6), 505-510 (2019).
- Willauer, A. N., et al. Clinical and molecular characterization of early-onset colorectal cancer. Cancer. 125 (12), 2002-2010 (2019).
- Watanabe, A., et al. A case of primary colonic signet ring cell carcinoma in a young man which preoperatively mimicked Phlebosclerotic colitis. Acta Med Okayama. 73 (4), 361-365 (2019).
- Kim, H., Kim, B. H., Lee, D., Shin, E. Genomic alterations in signet ring and mucinous patterned colorectal carcinoma. Pathol Res Pract. 215 (10), 152566(2019).
- Deng, X., et al. Neoadjuvant radiotherapy versus surgery alone for stage II/III mid-low rectal cancer with or without high-risk factors: A prospective multicenter stratified randomized trial. Ann Surg. 272 (6), 1060-1069 (2020).
- Buk Cardoso, L., et al. Machine learning for predicting survival of colorectal cancer patients. Sci Rep. 13 (1), 8874(2023).
- Monterrubio-Gómez, K., Constantine-Cooke, N., Vallejos, C. A. A review on statistical and machine learning competing risks methods. Biom J. 66 (2), e2300060(2024).
- Kim, H. J., Choi, G. S. Clinical implications of lymph node metastasis in colorectal cancer: Current status and future perspectives. Ann Coloproctol. 35 (3), 109-117 (2019).
- Xu, T., et al. Log odds of positive lymph nodes is an excellent prognostic factor for patients with rectal cancer after neoadjuvant chemoradiotherapy. Ann Transl Med. 9 (8), 637(2021).
- Chen, Y. R., et al. Prognostic performance of different lymph node classification systems in young gastric cancer. J Gastrointest Oncol. 12 (4), 285-1300 (2021).
- Bouvier, A. M., et al. How many nodes must be examined to accurately stage gastric carcinomas? Results from a population based study. Cancer. 94 (11), 2862-2866 (2002).
- Coburn, N. G., Swallow, C. J., Kiss, A., Law, C. Significant regional variation in adequacy of lymph node assessment and survival in gastric cancer. Cancer. 107 (9), 2143-2151 (2006).
- Li Destri, G., Di Carlo, I., Scilletta, R., Scilletta, B., Puleo, S. Colorectal cancer and lymph nodes: the obsession with the number 12. World J Gastroenterol. 20 (8), 1951-1960 (2014).
- Dinaux, A. M., et al. Outcomes of persistent lymph node involvement after neoadjuvant therapy for stage III rectal cancer. Surgery. 163 (4), 784-788 (2018).
- Sun, Y., Zhang, Y., Huang, Z., Chi, P. Prognostic implication of negative lymph node count in ypN+ rectal cancer after neoadjuvant chemoradiotherapy and construction of a prediction nomogram. J Gastrointest Surg. 23 (5), 1006-1014 (2019).
- Xu, Z., Jing, J., Ma, G. Development and validation of prognostic nomogram based on log odds of positive lymph nodes for patients with gastric signet ring cell carcinoma. Chin J Cancer Res. 32 (6), 778-793 (2020).
- Scarinci, A., et al. The impact of log odds of positive lymph nodes (LODDS) in colon and rectal cancer patient stratification: a single-center analysis of 323 patients. Updates Surg. 70 (1), 23-31 (2018).
- Nitsche, U., et al. Prognosis of mucinous and signet-ring cell colorectal cancer in a population-based cohort. J Cancer Res Clin Oncol. 142 (11), 2357-2366 (2016).
- Kang, H., O'Connell, J. B., Maggard, M. A., Sack, J., Ko, C. Y. A 10-year outcomes evaluation of mucinous and signet-ring cell carcinoma of the colon and rectum. Dis Colon Rectum. 48 (6), 1161-1168 (2005).
- Sung, C. O., et al. Clinical significance of signet ring cells in colorectal mucinous adenocarcinoma. Mod Pathol. 21 (12), 1533-1541 (2008).
- Alvi, M. A., et al. Molecular profiling of signet ring cell colorectal cancer provides a strong rationale for genomic targeted and immune checkpoint inhibitor therapies. Br J Cancer. 117 (2), 203-209 (2017).
- Brownlee, S., et al. Evidence for overuse of medical services around the world. Lancet. 390 (10090), 156-168 (2017).
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoThis article has been published
Video Coming Soon
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados