Method Article
Vergleich der prädiktiven Leistung von drei Lymphknoten-Staging-Systemen beim kolorektalen Siegelringzellkarzinom auf Basis eines maschinellen Lernmodells
* Diese Autoren haben gleichermaßen beigetragen
In diesem Artikel
Zusammenfassung
In dieser Studie werden prognostische Systeme für Patienten mit kolorektalem Siegelringzellkarzinom unter Verwendung von Modellen des maschinellen Lernens und konkurrierenden Risikoanalysen evaluiert. Es identifiziert die logarithmische Wahrscheinlichkeit positiver Lymphknoten als überlegenen Prädiktor im Vergleich zum pN-Staging, zeigt eine starke Vorhersageleistung und unterstützt die klinische Entscheidungsfindung durch robuste Überlebensvorhersagewerkzeuge.
Zusammenfassung
Der Lymphknotenstatus ist ein kritischer prognostischer Prädiktor für Patienten; Die Prognose des kolorektalen Siegelringzellkarzinoms (SRCC) hat jedoch nur wenig Aufmerksamkeit erhalten. In dieser Studie wird die prognostische Vorhersagefähigkeit der logarithmischen Wahrscheinlichkeiten positiver Lymphknoten (LODDS), des Lymphknotenverhältnisses (LNR) und des pN-Stagings bei SRCC-Patienten unter Verwendung von maschinellen Lernmodellen (Random Forest, XGBoost und Neural Network) neben konkurrierenden Risikomodellen untersucht. Relevante Daten wurden aus der Datenbank Surveillance, Epidemiology, and End Results (SEER) extrahiert. Für die Modelle des maschinellen Lernens wurden prognostische Faktoren für das krebsspezifische Überleben (CSS) durch univariate und multivariate Cox-Regressionsanalysen identifiziert, gefolgt von der Anwendung von drei Methoden des maschinellen Lernens - XGBoost, RF und NN -, um das optimale Lymphknoten-Staging-System zu ermitteln. Im konkurrierenden Risikomodell wurden univariate und multivariate konkurrierende Risikoanalysen verwendet, um prognostische Faktoren zu identifizieren, und ein Nomogramm wurde erstellt, um die Prognose von SRCC-Patienten vorherzusagen. Die Fläche unter der Betriebskennlinie des Empfängers (AUC-ROC) und die Kalibrierungskurven wurden verwendet, um die Leistung des Modells zu bewerten. Insgesamt wurden 2.409 SRCC-Patienten in diese Studie eingeschlossen. Um die Wirksamkeit des Modells zu validieren, wurde eine zusätzliche Kohorte von 15.122 Darmkrebspatienten, ohne SRCC-Fälle, für die externe Validierung eingeschlossen. Sowohl die Modelle des maschinellen Lernens als auch das konkurrierende Risikonomogramm zeigten eine starke Leistung bei der Vorhersage von Überlebensergebnissen. Im Vergleich zum pN-Staging zeigten die LODDS-Staging-Systeme eine überlegene prognostische Fähigkeit. Bei der Evaluierung erreichten Modelle des maschinellen Lernens und konkurrierende Risikomodelle eine hervorragende Vorhersageleistung, die sich durch eine gute Unterscheidung, Kalibrierung und Interpretierbarkeit auszeichnete. Unsere Ergebnisse können dazu beitragen, die klinische Entscheidungsfindung für Patienten zu informieren.
Einleitung
Darmkrebs (CRC) ist weltweit der dritthäufigste bösartige Tumor 1,2,3. Das Siegelringzellkarzinom (SRCC), ein seltener Subtyp des Darmkrebses, umfasst etwa 1% der Fälle und zeichnet sich durch reichlich intrazelluläres Muzin aus, das den Zellkern verdrängt 1,2,4. SRCC ist oft mit jüngeren Patienten assoziiert, hat eine höhere Prävalenz bei Frauen und hat bei der Diagnose fortgeschrittene Tumorstadien. Im Vergleich zum kolorektalen Adenokarzinom zeigt das SRCC eine schlechtere Differenzierung, ein höheres Risiko für Fernmetastasen und eine 5-Jahres-Überlebensrate von nur 12%-20%5,6. Die Entwicklung eines genauen und effektiven Prognosemodells für SRCC ist entscheidend für die Optimierung von Behandlungsstrategien und die Verbesserung der klinischen Ergebnisse.
Diese Studie zielt darauf ab, ein robustes Prognosemodell für SRCC-Patienten unter Verwendung fortschrittlicher statistischer Ansätze, einschließlich maschinellem Lernen (ML) und konkurrierenden Risikomodellen, zu erstellen. Diese Methoden können komplexe Beziehungen in klinischen Daten berücksichtigen, bieten individuelle Risikobewertungen und übertreffen traditionelle Methoden in Bezug auf die Vorhersagegenauigkeit. Modelle für maschinelles Lernen wie Random Forest, XGBoost und neuronale Netze zeichnen sich durch die Verarbeitung hochdimensionaler Daten und die Identifizierung komplizierter Muster aus. Studien haben gezeigt, dass KI-Modelle die Überlebensergebnisse bei Darmkrebs effektiv vorhersagen, was das Potenzial von ML in klinischen Anwendungen unterstreicht 7,8. Ergänzend zu ML berücksichtigen konkurrierende Risikomodelle mehrere Ereignistypen, wie z. B. krebsspezifische Mortalität im Vergleich zu anderen Todesursachen, um die Überlebensanalyse zu verfeinern. Im Gegensatz zu herkömmlichen Methoden wie dem Kaplan-Meier-Schätzer schätzen konkurrierende Risikomodelle die marginale Wahrscheinlichkeit von Ereignissen in Gegenwart konkurrierender Risiken genau ab und ermöglichen so genauere Überlebensbewertungen8. Die Integration von ML und konkurrierender Risikoanalyse verbessert die Vorhersageleistung und bietet ein leistungsstarkes Framework für personalisierte Prognosetools in SRCC 9,10,11.
Lymphknotenmetastasen beeinflussen die Prognose und das Rezidiv bei Darmkrebspatienten maßgeblich. Während die Beurteilung des N-Stadiums in der TNM-Klassifikation kritisch ist, kann eine unzureichende Lymphknotenuntersuchung - die in 48 % bis 63 % der Fälle berichtet wird - zu einer Unterschätzung der Krankheit führen. Um dies zu beheben, wurden alternative Ansätze wie die Lymphknotenzahl (LNR) und die logarithmischen Chancen positiver Lymphknoten (LODDS) eingeführt. LNR, das Verhältnis von positiven Lymphknoten (PLNs) zu Gesamtlymphknoten (TLNs), wird weniger von der TLN-Anzahl beeinflusst und dient als prognostischer Faktor bei Darmkrebs. LODDS, das logarithmische Verhältnis von PLNs zu negativen Lymphknoten (NLNs), hat sowohl bei Magen-SRCC als auch bei Darmkrebs eine überlegene Vorhersagefähigkeit gezeigt10,11. Maschinelles Lernen wird zunehmend in der Onkologie eingesetzt, wobei Modelle die Risikostratifizierung und die prognostischen Vorhersagen bei verschiedenen Krebsarten, einschließlich Brust-, Prostata- und Lungenkrebs, verbessern 12,13,14. Die Anwendung bei kolorektalem SRCC ist jedoch nach wie vor begrenzt.
Diese Studie versucht, diese Lücke zu schließen, indem LODDS mit ML und konkurrierenden Risikomodellen integriert wird, um ein umfassendes Prognosewerkzeug zu schaffen. Durch die Bewertung des prognostischen Wertes von LODDS und den Einsatz fortschrittlicher prädiktiver Techniken zielt diese Forschung darauf ab, die klinische Entscheidungsfindung zu verbessern und die Ergebnisse für SRCC-Patienten zu verbessern.
Protokoll
Diese Studie bezieht sich nicht auf die ethische Zustimmung und Zustimmung zur Teilnahme. Die in dieser Studie verwendeten Daten wurden aus Datenbanken gewonnen. Wir schlossen Patienten ein, bei denen zwischen 2004 und 2015 ein kolorektales Siegelringzellkarzinom diagnostiziert wurde, sowie andere Arten von Darmkrebs. Zu den Ausschlusskriterien gehörten Patienten mit einer Überlebenszeit von weniger als einem Monat, Patienten mit unvollständigen klinisch-pathologischen Informationen und Fälle, in denen die Todesursache unklar oder nicht spezifiziert war.
1. Datenerfassung
- Laden Sie SEER herunter. Laden Sie die Statistiksoftware 8.4.3 von der SEER-Datenbank-Website (http://seer.cancer.gov/about/overview.html) herunter. Nachdem Sie sich bei der Software angemeldet haben, klicken Sie auf Case List Session > Data und wählen Sie die Datenbank Incidence SEER Research Plus Data, 17 Registries, Nov 2021 Sub (2000-2019) aus.
- Klicken Sie auf Auswahl > Bearbeiten und wählen Sie {Rasse, Geschlecht, Jahr Dx. Jahr der Diagnose} = '2004', '2005', '2006', '2007', '2008', '2009', '2010', '2011', '2012', '2013', '2014', '2015' UND {Standort und Morphologie. Standort-Rekodierung ICD-O-3/WHO 2008} = '8490/3'.
- Klicken Sie dann auf Tabelle und wählen Sie in der Benutzeroberfläche für verfügbare Variablen die Option Alter neu kodieren mit Einzelalter und 100+, Geschlecht, Ehe, Standort neu kodieren ICD-O-3/WHO 2008, CS Tumorgröße, Regional nodes_examined (1988+), Regional nodes_positive (1988+), Abgeleitete AJCC Stage Group, 6. Auflage (2004-2015), Abgeleitetes AJCC T, 6. Aufl. (2004-2015), Abgeleitetes AJCC N, 6. Aufl. (2004-2015), Abgeleitetes AJCC M, 6. Auflage (2004-2015), CEA, Strahlen-Rekodierung, Chemotherapie-Rekodierung (ja, nein/unk), SEER-ursachenspezifische Todesklassifikation, Rekodierung des Vitalstatus (Studien-Cutoff verwendet), Überlebensmonate, Jahr der Diagnose.
- Klicken Sie abschließend auf Ausgabe, benennen Sie die Daten und klicken Sie auf Ausführen , um die Daten auszugeben und zu speichern. Der detaillierte Einschlussprozess ist in Abbildung 1 dargestellt.
- Laden Sie Daten von Darmkrebspatienten, mit Ausnahme von SRCC-Fällen, für eine spätere externe Validierung herunter. Klicken Sie auf Auswahl > Bearbeiten und wählen Sie {Rasse, Geschlecht, Jahr Dx. Jahr der Diagnose} = '2004', '2005', '2006', '2007', '2008', '2009', '2010', '2011', '2012', '2013', '2014', '2015' UND {Primary Site - labeled} = 'C18-C20'. Wiederholen Sie die Schritte 1.3 und 1.4, um klinisch pathologische Informationen zu erhalten und Proben mit {Lokalisation und Morphologie auszuschließen. Site recode ICD-O-3/WHO 2008} = '8490/3' aus der heruntergeladenen Datei.
- Verarbeiten Sie zu Vergleichszwecken mehrere Variablen. Klassifizieren Sie den Lymphknotenstatus sowohl anhand des Lymphknotenverhältnisses (LNR) als auch des Logarithmus der Wahrscheinlichkeit positiver Lymphknoten (LODDS).
- Definieren Sie LNR als das Verhältnis von positiven Lymphknoten (PLNs) zu Gesamtzahl der Lymphknoten (TLNs). Berechnen Sie den LODDS-Wert mit der Formel:
loge(Anzahl der PLNs + 0,5) / (Anzahl der negativen Lymphknoten (NLNs) + 0,5)
wobei 0,5 hinzugefügt wurde, um ein unendliches Ergebnis zu verhindern. Die Cut-off-Werte für LNR, LODDS und Tumorgröße wurden mit der X-Tile-Software (Version 3.6.1) auf Basis der minimalen P-Wert-Methode bestimmt.
- Definieren Sie LNR als das Verhältnis von positiven Lymphknoten (PLNs) zu Gesamtzahl der Lymphknoten (TLNs). Berechnen Sie den LODDS-Wert mit der Formel:
- Öffnen Sie die X-Tile-Software, klicken Sie auf Datei > Öffnen und wählen Sie die Datendatei aus, um sie in die Software zu importieren. Sobald die Daten geladen sind, ordnen Sie die Variablen zu: Zensor entspricht dem Überlebensstatus, die Überlebenszeit entspricht der Überlebenszeit und marker1 ist die zu analysierende Variable, um sicherzustellen, dass die Daten korrekt übereinstimmen.
- Klicken Sie dann auf Do > Kaplan-Meier > Marker1 , um die Kaplan-Meier-Überlebensanalyse durchzuführen und die Überlebenskurve zu generieren. Basierend auf der Trennung der Kaplan-Meier-Überlebenskurven, der statistischen Signifikanz (z.B. p-Wert) und der klinischen Relevanz wird der optimale Cut-off-Wert ermittelt und schließlich die Analyseergebnisse aufgezeichnet bzw. exportiert.
- Unterteilen Sie LNR in drei Gruppen: LNR 1 (≤0,16), LNR 2 (0,16 - 0,78) und LNR 3 (≥ 0,78). Kategorisieren Sie die Patienten basierend auf LODDS in drei Gruppen: LODDS 1 (≤ -1,44), LODDS 2 (-1,44 - 0,86) und LODDS 3 (≥ 0,86).
- Klassifizieren Sie die Tumorgröße in drei Kategorien: ≤ 3,5 cm, 3,5 - 5,5 cm und ≥ 5,5 cm. Konvertieren Sie das Alter von einer kontinuierlichen in eine kategoriale Variable. Kategorisieren Sie das Alter der Patienten zum Zeitpunkt der Erstdiagnose als ≥60 Jahre und <60 Jahre. Klassifizieren Sie die Tumorlokalisation basierend auf der Verteilung von Siegelringzellkarzinomen (SRCC) als rechter Dickdarm, linker Dickdarm und Rektum. Der rechte Dickdarm umfasst den Blinddarm, den aufsteigenden Dickdarm, die Leberflexur und den Dickdarm transversal, während der linke Dickdarm die Milzflexur, den absteigenden Dickdarm, den Sigma und den Rektosigmoidübergang umfasst.
- Für diese Studie wurden insgesamt 2409 geeignete Patientendaten mit SRCC nach dem Zufallsprinzip einer Trainingskohorte (N = 1686) und einer Validierungskohorte (N = 723) im Verhältnis 7:3 zugeordnet. Verwenden Sie den folgenden Code für die zufällige Aufteilung, und beziehen Sie data.csv aus der SEER-Datenbank. Die Dateien, die nach der zufälligen Aufteilung generiert werden, werden für die weitere Analyse verwendet.
Bibliothek(Einfügezeichen)
Daten <- read.csv("data.csv")
set.seed(123)
train_indices <- createDataPartition(data$variable, p = 0,7, list = FALSE)
train_data <- Daten[train_indices, ]
test_data <- Daten[-train_indices, ]
write.csv(train_data, "traindata.csv", row.names = FALSCH)
write.csv(test_data, "testdata.csv", row.names = FALSCH)
2. Entwicklung und Verifizierung von ML-Modellen
- Laden Sie RStudio (2024.04.2+764) und R Software (4.4.1) herunter. Öffnen Sie RStudio, um die R-Software auszuführen. Klicken Sie auf Neue Datei und wählen Sie R-Skript aus, um eine neue R-Programmierschnittstelle zu erstellen. Geben Sie den entsprechenden Code in den Code-Editor ein und klicken Sie auf Ausführen , um den Code auszuführen.
- Verwenden Sie den folgenden Code, um die Variablen zu überprüfen, die in den ML-Modellen durch die Cox-Regressionsanalyse enthalten sind. Untersuchen Sie außerdem die Auswirkungen von LODDS-, LNR- und pN-Staging auf das krebsspezifische Überleben (CSS) bei SRCC-Patienten. Der traindata.csv sind Daten, die aus der SEER-Datenbank abgerufen werden.
Bibliothek("Überleben")
Bibliothek ("Survminer")
Bibliothek("rms")
Bibliothek("dplyr")
Daten <- read.csv("traindata.csv")
data$time=as.numeric(data$time)
data$status=as.numeric(daten$status)
Variablen <- c("Geschlecht", "Alter", "Rasse", "Ehe", "Phase", "T", "N", "M", "Tumor_size", "LNR", "LODDS", "CEA", "Bestrahlung", "Chemotherapie", "Standort")
Daten <- Daten %>%
mutate(across(all_of(Variablen), as.factor))
cox=coxph(Surv(Zeit, Status) ~ Daten$T, Daten = Daten)
cox$Koeffizienten
pval=anova(cox)$Pr[2]
clean_data=Daten[,c(1:12, 14:18)]
get_coxVariable=Funktion(your_data,Index){cox_list=c() k=1
for (i in 1:index) {mod=coxph(Surv(Zeit, Status) ~ your_data[,i],data=your_data) pval=anova(mod)$Pr[2] print(pval) print(colnames(your_data)[i]) if (pval<0.05) {cox_list[k]=colnames(your_data)[i] k=k+1}}return(cox_list)}
variable_select=get_coxVariable(clean_data,15)
for(i in 1:15){print(variable_select[i])}
for (var in variable_select) {formula <- as.formula(paste("Surv(Zeit, Status) ~", var))cox_model <- coxph(Formel, Daten = Daten) print(summary(cox_model))
ggforest(Steuermann)
Variablen <- c("Geschlecht", "Alter", "Rasse", "Ehe", "Phase", "T", "N", "M", "Tumor_size", "LNR", "LODDS", "Chemotherapie")
Daten <- Daten %>%
mutate(across(all_of(Variablen), as.factor))
cox=coxph(Surv(Zeit, Status) ~ Geschlecht+Alter+Rasse+Ehe+T+N+M+Tumor_size+LNR+
LODDS+Chemotherapie,Daten = Daten)
ggforest(cox,data = Daten)
ggplot_forest <- ggforest(cox, Daten = Daten) - Verwenden Sie den folgenden Code, um die prognostischen Vorhersagefähigkeiten von drei LN-Systemen (LODDS, LNR und pN-Staging) in den Trainings-, Validierungs- und externen Validierungskohorten zu vergleichen.
Bibliothek(RMS)
Bibliothek(Überleben)
Bibliothek(Survminer)
library(riskRegression)
Bibliothek(gt)
train_data <- read.csv("train_data123.csv")
validation_data <- read.csv("test_data123.csv")
dd <- datadist(train_data)
Optionen(datavert = "dd")
model_LNR <- cph(Surv(Zeit, Status) ~ LNR, Daten = train_data, x = WAHR, y = WAHR)
model_LODDS <- cph(Surv(Zeit, Status) ~ LODDS, Daten = train_data, x = WAHR, y = WAHR)
model_pN <- cph(Surv(Zeit, Status) ~ N, Daten = train_data, x = WAHR, y = WAHR)
calculate_performance <- function(model, data) {pred <- predict(model, newdata = data) c_index_result <- concordance(Surv(data$time, data$status) ~ pred) c_index <- c_index_result$concordance aic <- AIC(model) bic <- BIC(model) return(c(C_index = round(c_index, 3), AIC = round(aic, 2), BIC = round(bic, 2)))}
calculate_performance <- function(model, data) {pred <- predict(model, newdata = data, type = "lp") concordance_result <- concordancefit(Surv(data$time, data$status), x = pred) c_index <- concordance_result$concordance ci_lower <- c_index - 1.96 * sqrt(concordance_result$var) ci_upper <- c_index + 1.96 * sqrt(concordance_result$var) aic <- AIC(model) bic <- BIC(model) return(c(C_Index = round(c_index, 3), CI_Lower = Runde(ci_lower, 3), CI_Upper = Runde(ci_upper, 3), AIC = Runde(AIC, 2), BIC = Runde(bic, 2)))}
train_LNR <- calculate_performance(model_LNR, train_data)
train_LODDS <- calculate_performance(model_LODDS, train_data)
train_pN <- calculate_performance (model_pN, train_data)
model_LNR_val <- cph(Surv(Zeit, Status) ~ LNR, Daten = validation_data, x = WAHR, y = WAHR)
model_LODDS_val <- cph(Surv(Zeit, Status) ~ LODDS, Daten = validation_data, x = WAHR, y = WAHR)
model_pN_val <- cph(Surv(Zeit, Status) ~ N, Daten = validation_data, x = WAHR, y = WAHR)
val_LNR <- calculate_performance (model_LNR_val, validation_data)
val_LODDS <- calculate_performance(model_LODDS_val, validation_data)
val_pN <- calculate_performance (model_pN_val, validation_data)
Ergebnisse <- data.frame(Variable = c("LNR", "LODDS", "pN"), Training_C_Index = c(paste(train_LNR["C_Index"], "("train_LNR["CI_Lower"], ", ", ", train_LNR["CI_Upper"], ")", sep = ""), paste(train_LODDS["C_Index"], "(", train_LODDS["CI_Lower"], ", ", train_LODDS["CI_Upper"], ")", sep = ""), paste(train_pN["C_Index"], "(", train_pN["CI_Lower"], ", ", train_pN["CI_Upper"], ")", sep = "")"), Training_AIC = c(train_LNR["AIC"], train_LODDS["AIC"], train_pN["AIC"]), Training_BIC = c(train_LNR["BIC"], train_LODDS["BIC"], train_pN["BIC"]), Validation_C_Index = c(paste(val_LNR["C_Index"], "(", val_LNR["CI_Lower"], ", ", val_LNR["CI_Upper"], ")", sep = ""), paste(val_LODDS["C_Index"], "(", val_LODDS["CI_Lower"], ", ", val_LODDS["CI_Upper"], ")", sep = ""), paste(val_pN["C_Index"], "(", val_pN["CI_Lower"], "[""], ", ", val_pN["CI_Upper"], ")", sep = "")"), Validation_AIC = c(val_LNR["AIC"], val_LODDS["AIC"], val_pN["AIC"]), Validation_BIC = c(val_LNR["BIC"], val_LODDS["BIC"], val_pN["BIC"]))
results_table <- GT(Ergebnisse) %>%
tab_header(title = "Vorhersageleistung der drei Lymphknoten-Staging-Systeme") %>%
cols_label(Variable = "Variable",Training_C_Index = "C-Index (95% CI) (Training)", Training_AIC = "AIC (Training)", Training_BIC = "BIC (Training)", Validation_C_Index = "C-Index (95% CI) (Validierung)", Validation_AIC = "AIC (Validierung)", Validation_BIC = "BIC (Validierung)")
write.csv(Ergebnisse, "prediction_performance.csv", row.names = FALSCH) - Verwenden Sie den folgenden Code, um ein XGBoost-Modell zu erstellen und Balkendiagramme der relativen Wichtigkeit von Variablen zu generieren, um so die Wichtigkeit der drei LN-Systeme zu vergleichen. Generieren Sie auf ähnliche Weise ROC-Kurven und Kalibrierungskurven. Die Daten werden aus der SEER-Datenbank bezogen.
Bibliothek(xgboost)
Bibliothek(Einfügezeichen)
Bibliothek(pROC)
train_data <- read.csv("train_data.csv")
test_data <- read.csv("test_data.csv")
train_matrix <- XGB. DMatrix(data = as.matrix(train_data[, c('Alter', 'T', 'N', 'M', 'LODDS', 'Chemotherapie')]), label = train_data$status)
test_matrix <- XGB. DMatrix(data = as.matrix(test_data[, c('Alter', 'T', 'N', 'M', 'LODDS', 'Chemotherapie')]), label = test_data$status)
params <- list(booster = "gbtree", objective = "binary:logistic", eval_metric = "auc", eta = 0.1, max_depth = 6, subsample = 0.8, colsample_bytree = 0.8)
xgb_model <- xgb.train(params = params, data = train_matrix, nrounds = 100, watchlist= list(train = train_matrix), ausführlich = 1)
pred_probs <- predict(xgb_model, newdata = test_matrix)
pred_labels <- ifelse(pred_probs > 0,5, 1, 0)
conf_matrix <- confusionMatrix(as.factor(pred_labels), as.factor(test_data$status))
roc_curve <- roc(test_data$status, pred_probs)
auc_value <- AUC(roc_curve)
ci_auc <- ci.auc(roc_curve)
sensitivity <- conf_matrix$byClass["Empfindlichkeit"]
Spezifität <- conf_matrix$byClass["Spezifität"]
Genauigkeit <- conf_matrix$gesamt["Genauigkeit"]
ppv <- conf_matrix$byClass["Pos Pred Wert"]
npv <- conf_matrix$byClass["Neg Pred-Wert"]
result_table <- data.frame(Modell = "XGBoost", AUC = sprintf("%.3f (%.3f-%.3f)", auc_value, ci_auc[1], ci_auc[3]), Sensitivität = sprintf("%.3f", Sensitivität), Spezifität = sprintf("%.3f", Spezifität), Genauigkeit = sprintf("%.3f", Genauigkeit), PPV = sprintf("%.3f", ppv), NPV = sprintf("%.3f", npv))
write.csv(result_table, "xgboost_model_performance.csv", row.names = FALSCH)
roc_df <- data.frame(FPR = 1 - roc_curve$Spezifitäten, TPR = roc_curve$sensitivitäten)
roc_plot <- ggplot(roc_df, aes(x = FPR, y = TPR)) +geom_line(color = "steelblue", size = 1.2) + geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "gray") + annotate("text", x = 0.9, y = 0.2, label = paste("AUC =", round(auc_value, 3)), size = 5, color = "black") + labs(title = "ROC-Kurve für XGBoost-Modell", x = "Falsch-Positiv-Rate", y = "True-Positive-Rate") + theme_minimal() + theme(panel.border = element_rect(color = "schwarz", Füllung = NA, Größe = 1))
calibration_data <- data.frame(Status = as.factor(test_data$status), pred_probs = pred_probs)
calib_model <- calibration(Status ~ pred_probs, Daten = calibration_data, Klasse = "1", Schnitte = 5)
ggplot(calib_model$data, aes(x = Mittelpunkt, y = Prozent)) + geom_line(color = "steelblue", size = 1) + geom_point(color = "red", size = 2) + geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "black") +labs(title = "Kalibrierungskurve für das XGBoost-Modell", x = "Vorhergesagte Wahrscheinlichkeit", y = "Beobachteter Anteil") + theme_minimal() + theme(panel.border = element_rect(color = "black", fill = NA, size = 0.5)) - Verwenden Sie den folgenden Code, um ein RF-Modell zu erstellen und Balkendiagramme der relativen Wichtigkeit von Variablen zu generieren und so die Bedeutung der drei LN-Systeme zu vergleichen. Generieren Sie auf ähnliche Weise ROC-Kurven und Kalibrierungskurven. Die Daten stammen aus der SEER-Datenbank.library(randomForest)
Bibliothek (DPLYR)
Bibliothek(ggplot2)
Bibliothek(pROC)
Bibliothek(Einfügezeichen)
Bibliothek(RMS)
Trainset <- read.csv("train_data.csv")
Getestet <- read.csv("test_data.csv")
trainset$status=Faktor(trainset$status)
Variablen1 <- c("Alter", "T", "N", "M", "LODDS", "Chemotherapie")
Trainset <- Trainset %>%
mutate(across(all_of(Variablen1), as.numerisch))
getestet$status=faktor(getestet$status)
Getestet <- getestet %>%
mutate(across(all_of(Variablen1), as.numerisch))
RF=randomForest(trainset$status ~ Alter + T + N + M + LODDS + Chemotherapie, data=trainset,ntree=100,importance=TRUE,proximity=TRUE)
imp=Wichtigkeit(RF)
varImpPlot(RF)
impvar=Zeilennamen(IMP)[Reihenfolge(IMP[,4],abnehmend = WAHR)]
importance_df <- as.data.frame(imp)
importance_df$Variablen <- Zeilennamen(importance_df)
importance_plot <- ggplot(importance_df, aes(x = reorder(Variablen, MeanDecreaseAccuracy), y = MeanDecreaseAccuracy)) +geom_bar(stat = "identity", fill = "steelblue") +coord_flip() + labs(title = "Variablenbedeutung", x = "Variablen", y = "Genauigkeit der mittleren Abnahme") + theme_minimal()
pred_probs <- predict(RF, Testset, Typ = "prob")[,2]
roc_obj <- roc(testset$status, pred_probs)
auc_value <- AUC(roc_obj)
roc_plot <- ggplot() +geom_line(aes(x = 1 - roc_obj$Spezifitäten, y = roc_obj$sensitivitäten), color = "steelblue", size = 1.2) +geom_abline(intercept = 0, slope = 1, linetype = "gestrichelt", color = "grau") + annotate("text", x = 0.8, y = 0.2, label = paste("AUC =", round(auc_value, 3)), color = "black", size = 5, hjust = 0) + labs(title = "ROC-Kurve für Random Forest Model", x = "Falsch-Positiv-Rate", y = "Wahr-Positiv-Rate") +theme_minimal() + theme(panel.border = element_rect(color = "black", fill = NA, size = 1))
calibration_data <- data.frame(pred_probs = pred_probs, status = getestet$status)
calib_model <- Kalibrierung(Status ~ pred_probs, Daten = calibration_data, Klasse = "1", Schnitte = 5)
calib_df <- as.data.frame(calib_model[["Daten"]])
calib_df$mittlerer <- calib_df$Mittelwert
calib_df$Percent <- calib_df$Percent
calibration_plot <- ggplot(calib_df, aes(x = mid, y = Prozent)) + geom_line(color = "steelblue", size = 1.2) + geom_point(color = "steelblue", size = 3) + geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "black", size = 0.8) + labs(title = "Kalibrierungskurve für Random Forest", x = "Vorhergesagte Wahrscheinlichkeit", y = "tatsächliche Wahrscheinlichkeit") + theme_minimal() + theme(panel.border = element_rect(color = "schwarz", fill = NA, size = 1), plot.title = element_text(hjust = -0.05, vjust = -1.5, face = "bold", size = 12) )
rf_probs <- predict(RF, newdata=getestet, type="prob")[, 2]
rf_auc <- roc(getestet$status, rf_probs)
auc_value <- AUC(rf_auc)
ci_auc <- ci.auc(rf_auc)
rf_predictions <- predict(RF, newdata=getestet)
conf_matrix <- confusionMatrix(rf_predictions, getestet$status)
sensitivity <- conf_matrix$byClass["Empfindlichkeit"]
Spezifität <- conf_matrix$byClass["Spezifität"]
Genauigkeit <- conf_matrix$gesamt["Genauigkeit"]
ppv <- conf_matrix$byClass["Pos Pred Wert"]
npv <- conf_matrix$byClass["Neg Pred-Wert"]
result_table <- data.frame(Modell = "RF", AUC = sprintf("%.3f (%.3f-%.3f)", auc_value, ci_auc[1], ci_auc[3]), Sensitivität = sprintf("%.3f", Sensitivität), Spezifität = sprintf("%.3f", Spezifität), Genauigkeit = sprintf("%.3f", Genauigkeit), PPV = sprintf("%.3f", ppv), NPV = sprintf("%.3f", npv))
write.csv(result_table, "RF_model_performance.csv", row.names = FALSCH) - Verwenden Sie den folgenden Code, um ein NN-Modell zu erstellen und Balkendiagramme der relativen Wichtigkeit von Variablen zu generieren und so die Bedeutung der drei LN-Systeme zu vergleichen. Generieren Sie auf ähnliche Weise ROC-Kurven und Kalibrierungskurven. Die Daten werden aus der SEER-Datenbank database.library (nnet) bezogen
Bibliothek(Einfügezeichen)
Bibliothek(pROC)
Bibliothek(ggplot2)
train_data <- read.csv("train_data.csv")
test_data <- read.csv("test_data.csv")
train_data$status <- as.factor(train_data$status)
test_data$status <- as.factor(test_data$status)
Eigenschaften <- c("Alter", "T", "N", "M", "LODDS", "Chemotherapie")
x_train <- train_data[, Funktionen]
y_train <- train_data$status
x_test <- test_data[, Funktionen]
y_test <- test_data$status
nn_model <- nnet(Status ~ Alter + T + N + M + LODDS + Chemotherapie, Daten = train_data, Größe = 5, Zerfall = 0,01, maxit = 200)
pred_probs <- predict(nn_model, newdata = x_test, type = "raw")
pred_labels <- ifelse(pred_probs > 0,5, 1, 0)
roc_curve <- roc(as.numeric(y_test), pred_probs)
auc_value <- AUC(roc_curve)
auc_ci <- ci.auc(roc_curve)
auc_text <- paste0(runde(auc_value, 3), " (", runde(auc_ci[1], 3), "-", runde(auc_ci[3], 3), ")")
conf_matrix <- confusionMatrix(as.factor(pred_labels), y_test)
Genauigkeit <- conf_matrix$gesamt["Genauigkeit"]
sensitivity <- conf_matrix$byClass["Empfindlichkeit"]
Spezifität <- conf_matrix$byClass["Spezifität"]
ppv <- conf_matrix$byClass["Pos Pred Wert"]
npv <- conf_matrix$byClass["Neg Pred-Wert"]
performance_table <- data.frame(Metrik = c("AUC (95% CI)", "Genauigkeit", "Sensitivität", "Spezifität", "PPV", "NPV"),Value = c(auc_text, round(Genauigkeit, 3), round(Sensitivität, 3), round(Spezifität, 3), round(ppv, 3), round(npv, 3)))
write.csv(performance_table, "NN_performance_table.csv", row.names = FALSCH)
roc_curve <- roc(y_test, pred_probs)
auc_value <- AUC(roc_curve)
roc_plot <- ggplot() + geom_line(aes(x = 1 - roc_curve$specificities, y = roc_curve$sensitivities), color = "steelblue", size = 1.2) +geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "gray") + annotate("text", x = 0.8, y = 0.2, label = paste("AUC =", round(auc_value, 3)), color = "black", size = 5, hjust = 0) + labs(title = "ROC-Kurve für neuronales Netzwerkmodell", x = "Falsch-Positiv-Rate", y = "Wahr-Positiv-Rate") + theme_minimal() + theme(panel.border = element_rect(color = "black", fill = NA, size = 1))
calibration_data <- data.frame(pred_probs = pred_probs, status = as.numeric(y_test) - 1)
calibration_data$pred_probs <- as.numeric(calibration_data$pred_probs)
calibration_data$calibration_bin <- cut(calibration_data$pred_probs, breaks = seq(0, 1, by = 0.2), include.lowest = TRUE)
calibration_summary <- Aggregat(Status ~ calibration_bin, Daten = calibration_data, FUN = Mittelwert)
calibration_summary$pred_mean <- aggregate(pred_probs ~ calibration_bin, data = calibration_data, FUN = mittelwert)$pred_probs
calibration_plot <- ggplot(calibration_summary, aes(x = pred_mean, y = status)) + geom_line(color = "steelblue", size = 1.2) + geom_point(color = "red", size = 3) + geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "black", size = 0.8) + labs(title = "Kalibrierungskurve für neuronale Netzwerke", x = "Vorhergesagte Wahrscheinlichkeit", y = "Tatsächliche Wahrscheinlichkeit") + theme_minimal() + theme(panel.border = element_rect(color = "schwarz", Füllung = NA, Größe = 1))
nn_var_importance <- varImp(nn_model)
importance_df <- data.frame(Merkmal = Zeilennamen(nn_var_importance), Wichtigkeit = nn_var_importance$Gesamt )
importance_plot <- ggplot(importance_df, aes(x = reorder(Merkmal, Wichtigkeit), y = Wichtigkeit)) + geom_bar(stat = "identity", fill = "steelblue") + coord_flip() + labs(title = "Variable Wichtigkeit für neuronale Netzwerke", x = "Funktionen", y = "Wichtigkeit") + theme_minimal()
3. Entwicklung und Verifizierung konkurrierender Risikomodelle
- Verwenden Sie den folgenden Code, um eine univariate Analyse durchzuführen und die CIF-Kurve (Cumulative Inzidence Function) darzustellen. Der data.csv sind Daten, die aus der SEER-Datenbank abgerufen werden. Die Methode zum Speichern nachfolgender Bilder ist die gleiche wie in diesem Schritt. Ersetzen Sie Site im Code nacheinander durch andere Faktoren, um eine univariate Analyse für alle Faktoren durchzuführen.
Bibliothek(TidyCMPRSK)
Bibliothek(gtZusammenfassung)
Bibliothek(ggplot2)
Bibliothek(ggsurvfit)
Bibliothek(ggprism)
AA <- read.csv("data.csv")
cif2 <- tidycmprsk::cuminc(Surv(Zeit, Status1) ~Standort, Daten = aa)
tidy(cif2;times = c(12,24,36,48,60))
tbl_cuminc(cif2, times =c(12,24,36,48,60), outcomes = c("CSS", "OSS"),estimate_fun = NULL, label_header = "**{time/12}-year cuminc**") %>%
add_p() %>%
add_n(Standort = "Ebene")
cuminc_plot <- ggcuminc(cif2, outcome = c("CSS", "OSS"), size = 1.5) + labs(x = "time") +add_quantile(y_value = 0.20, size = 1) + scale_x_continuous(breaks = seq(0, 84, by = 12), limits = c(0, 84)) +scale_y_continuous(label = scales::p ercent, breaks = seq(0, 1, by = 0.2), limits = c(0, 1)) + theme_prism() + theme(legend.position = c(0.2, 0.8), panel.grid = element_blank(),panel.grid.major.y = element_line(color = "grey80")) + theme(legend.spacing.x = unit(0.1, "cm"), legend.spacing.y = unit(0.01, "cm")) + theme(axis.ticks.length.x = unit(-0.2, "cm"), axis.ticks.x = element_line(color = "black", size = 1, lineend = 1)) + theme(axis.ticks.length.y = unit(-0.2, "cm"), axis.ticks.y = element_line(color = "black", size = 1, lineend = 1)) - Verwenden Sie den folgenden Code, um multivariate Analysen und Visualisierungen durchzuführen. Die data1.csv ergibt sich aus den Ergebnissen des vorherigen Codes. Nachdem Sie den Code ausgeführt haben, klicken Sie auf Exportieren, klicken Sie dann auf Als PDF speichern und schließlich auf Speichern , um das Bild zu speichern.
Bibliothek(TidyCMPRSK)
Bibliothek(gtZusammenfassung)
AA <-read.csv('data1.csv')
for (i in names(aa)[c(1:16, 19)]){aa[,i] <- as.factor(aa[,i])}
mul1Tabelle2 <- MUL1 %>%
gtsummary::tbl_regression(Exponentiat = WAHR) %>%
add_n(Standort = "Ebene"); Tabelle2
table_df <- as_tibble (Tabelle2)
Registerkarte <- Tabelle2$table_body
tab1 <- tab[,c(12,19,20,22:29)] - Verwenden Sie den folgenden Code, um das Nomogramm, die ROC-Kurve und die Kalibrierungskurve darzustellen. Nachdem Sie das Modell mit Daten aus der Trainingskohorte trainiert haben, verwenden Sie die Daten der Validierungskohorten und der externen Validierungskohorten, um model.library(QHScrnomo) zu validieren. Die externen Kohortendaten bestehen aus Proben von anderen Darmkrebsarten als dem Ringzellkarzinom, die in Schritt 1.4 ausgewählt wurden.
Bibliothek(RMS)
Bibliothek(timeROC)
Bibliothek(Überleben)
AA <-read.csv('data3.csv')
for (i in names(aa)[c(1:16, 19)]){aa[,i] <- as.factor(aa[,i])}
dd <- datadist(aa)
Optionen(datavert = "dd")
mul <- cph(Surv(time, Status1 == 1) ~ T + N + M + LODDS + Site, data = aa, x = TRUE, y = TRUE, surv = TRUE)
m3 <- crr.fit(mul, Fehlercode = 1, cencode = 0)
nomo <-Newlabels(fit = m3, labels =c(T="T", N= "N", M = "M", LODDS = "LODDS", Site = "Site"))
nomoc("N0","N1","N2"),M=c("M0";"M1"),LODDS=c
("LODDS1","LODDS2","LODDS3"),Site=
c("RSC","LSC","Rektum")))
nomogram.crr(fit =nomo , lp = F, xfrac = 0.3, fun.at =seq(from=0, to=1, by= 0.1) , failtime =c(12,36,60), funlabel = c("Kumulative CSS-Inzidenz über 1 Jahr","Kumulative CSS-Inzidenz über 3 Jahre","Kumulative CSS-Inzidenz über 5 Jahre"))
time_points <- c(12, 36, 60)
pred_risks_list <- lapply(time_points, function(time_point) {predict(m3, newdata = aa, type = "risk", time = time_point)})
pred_risks_df <- data.frame(do.call(cbind, pred_risks_list))
colnames(pred_risks_df) <- paste("risk_at", time_points, "Monate", sep = "_")
roc_1year <- timeROC(T = aa$time, delta = ifelse(aa$Status1 == "CSS", 1, 0), marker = pred_risks_df$risk_at_12_months, cause = 1, times = 12, iid = TRUE)
roc_3year <- timeROC(T = aa$time, delta = ifelse(aa$Status1 == "CSS", 1, 0), marker = pred_risks_df$risk_at_36_months, cause = 1, times = 36, iid = TRUE)
roc_5year <- timeROC(T = aa$time, delta = ifelse(aa$Status1 == "CSS", 1, 0), marker = pred_risks_df$risk_at_60_months, cause = 1,times = 60, iid = TRUE)
legend("bottomright",legend = c("1 Jahr CSS", "3 Jahre CSS", "5 Jahre CSS"), col = c("#BF1D2D", "#262626", "#397FC7"), lwd = 2)
sas.cmprsk(m3;time = 36)
set.seed(123)
aa$pro <- tenf.crr(m3,time = 36)
cindex(prob = aa$pro, fstatus = aa$Status1, ftime = aa$time, type = "crr", failcode = 1, cencode = 0, tol = 1e-20)
groupci(x=aa$pro, ftime = aa$time, fstatus = aa$Status1, failcode = 1, cencode = 0, ci = TRUE, g = 5, m = 1000, u = 36, xlab = "Vorhergesagte Wahrscheinlichkeit", ylab = "Tatsächliche Wahrscheinlichkeit", lty=1, lwd=2, col="#262626",xlim=c(0,1.0), ylim=c(0,1.0), add =TRUE)
Ergebnisse
Eigenschaften des Patienten
Diese Studie konzentrierte sich auf Patienten, bei denen kolorektale SRCC diagnostiziert wurde, wobei Daten aus der SEER-Datenbank aus den Jahren 2004 bis 2015 verwendet wurden. Zu den Ausschlusskriterien gehörten Patienten mit einer Überlebenszeit von weniger als einem Monat, Patienten mit unvollständigen klinisch-pathologischen Informationen und Fälle, in denen die Todesursache unklar oder nicht spezifiziert war. Insgesamt wurden 2409 kolorektale SRCC-Patienten, die die Einschlusskriterien erfüllten, nach dem Zufallsprinzip in eine Trainingskohorte (N = 1686) und eine Validierungskohorte (N = 723) eingeteilt. Die demographischen und klinischen Parameter der Trainings- und Validierungskohorten wurden mit der R-Software analysiert, wie in Tabelle 1 dargestellt. Unter allen eingeschlossenen Patienten war die Mehrheit über 60 Jahre alt, mit einer ähnlichen Anzahl von männlichen und weiblichen Patienten. Die meisten Patienten waren weiß. Mehr als die Hälfte der Patienten (56%) war verheiratet. Die Mehrzahl der Tumoren wurde als III-IV eingestuft (76%). Die meisten Patienten (82 %) hatten eine Tumorgröße von mehr als 3,5 Zentimetern, und die Mehrheit der Patienten gehörte zur LODDS1-Gruppe (42 %). In der gesamten Kohorte erhielt ein hoher Anteil der Patientinnen (53%) eine Chemotherapie. Primärtumoren waren hauptsächlich im rechten Dickdarm lokalisiert (67%). Nach der Randomisierung gab es statistisch keine signifikanten Unterschiede in den Ausgangsmerkmalen zwischen den beiden Gruppen.
Identifizierung der prognostischen klinischen Faktoren, die in den ML-Modellen enthalten sind
Wir haben zunächst signifikante Variablen für die Aufnahme in das Modell des maschinellen Lernens mit Hilfe der Cox-Regressionsanalyse untersucht. Die Ergebnisse der univariaten Cox-Regression zeigten, dass die Überlebenszeit signifikant mit bestimmten klinischen Variablen korrelierte, darunter Geschlecht, Alter, Rasse, Familienstand, AJCC-Staging, pT-Staging, pN-Staging, pM-Staging, Tumorgröße, CEA-Spiegel, LNR-Klassifikation, LODDS-Klassifikation und ob der Patient eine Strahlen- oder Chemotherapie erhielt (Tabelle 2). Bemerkenswert ist, dass LNR, LODDS und pN-Staging alle statistisch signifikante Hazard Ratios (HR) aufwiesen, was darauf hindeutet, dass diese drei LN-Staging-Systeme mit der Prognose verbunden sind. Eine anschließende multivariate Cox-Regressionsanalyse wurde durchgeführt, um den Zusammenhang zwischen pN-Staging, LODDS, LNR und CSS bei SRCC-Patienten weiter zu bestimmen. Die Ergebnisse zeigten, dass LODDS, LNR und pN-Status das CSS von SRCC-Patienten signifikant beeinflussten (Abbildung 2).
Vergleich von LN-Systemen
Die prädiktiven prognostischen Fähigkeiten der drei LN-Systeme waren sowohl in der Trainings-, Validierungs- als auch in der externen Validierungskohorte ähnlich (Proben von Darmkrebs mit Ausnahme des Ringzellkarzinoms, die in Schritt 1.4 ausgewählt wurden; Tabelle 3). In der Trainingskohorte betrugen die C-Indizes für LNR, LODDS und pN 0,309, 0,308 bzw. 0,337, während die C-Indizes in der Validierungskohorte 0,288, 0,279 bzw. 0,319 betrugen. In der externen Validierungskohorte betrugen die C-Indizes für LNR, LODDS und pN 0,419, 0,420 bzw. 0,424. Darüber hinaus betrugen die AIC-Werte für jedes System in der Trainingskohorte 12667,56, 12670,57 und 12731,89 und in der Validierungskohorte 4575,36, 4559,13 bzw. 4613,20. In der externen Validierungskohorte waren die AIC-Werte für jedes System wie folgt: 106554,68 für LODDS, 106581,85 für LNR und 106915,45 für pN-Staging. Diese Ergebnisse deuten darauf hin, dass es zwischen den drei Systemen nur minimale Unterschiede in der diskriminierenden Qualität gibt. Daher haben wir die Methoden des maschinellen Lernens RF, XGBoost und NN verwendet, um das optimale LN-System in Bezug auf die Vorhersagefähigkeit weiter zu bestimmen. Diese Analyse umfasste Variablen, die in der univariaten Cox-Regression signifikant waren, und mindestens ein multivariates Modell (pN, LODDS oder LNR) für die Konstruktion der Modelle des maschinellen Lernens, einschließlich pN, pT, pM, Alter, Rasse, LNR-Klassifikation, LODDS-Klassifikation und ob der Patient eine Strahlen- oder Chemotherapie erhielt.
Wir haben RF-, XGBoost- und NN-Modelle unter Verwendung des Trainingsdatasets erstellt. Die Wichtigkeitswerte für jede Variable sind in Abbildung 3 dargestellt. In RF und XGBoost wies LNR die höchste Bedeutung auf, während LODDS ebenfalls eine beträchtliche Bedeutung zeigte. Im NN-Modell zeigte LODDS jedoch eine bessere Vorhersagefähigkeit im Vergleich zu pN und LNR. Unter Berücksichtigung der kombinierten Ergebnisse der drei Ansätze des maschinellen Lernens kommen wir zu dem Schluss, dass das LODDS-System das beste System zur Beurteilung des LN-Status bei SRCC-Patienten sein könnte.
Leistung der ML-Modelle
Wie in Tabelle 4 und Abbildung 4A-C gezeigt, waren alle drei Modelle in der Lage, die Prognose effektiv vorherzusagen, und die AUCs der drei Modelle lagen im Testdatensatz zwischen 0,777 und 0,851 (XGBoost: AUC = 0,820, 95% CI = 0,789-0,851; RF: AUC = 0,819, 95% KI = 0,788-0,850; NN: AUC = 0,809, 95 % KI = 0,777-0,841). Die XGBoost-, RF- und NN-Modelle zeigten eine hohe Spezifität (0,82, 0,825, 0,815) und Genauigkeit (0,762, 0,763, 0,757). Die Kalibrierkurven sind in Abbildung 5D-F dargestellt.
Aufbau und Validierung eines wettbewerbsfähigen Risikomodells
Da die ML-Modelle den Einfluss konkurrierender Risikofaktoren nicht berücksichtigten, haben wir ein konkurrierendes Risikomodell erstellt, um das LN-System zu identifizieren, das in Bezug auf die Vorhersagefähigkeit am besten abgeschnitten hat. Das krebsspezifische Überleben (CSS) stellt den Tod durch Krebs dar, während das Gesamtüberleben (OSS) Todesfälle aus anderen Ursachen berücksichtigt, die als konkurrierende Risikoereignisse dienen. Wir verwendeten univariate und multivariate konkurrierende Risikomodelle, um die prädiktiven Faktoren für CSS in der Trainingskohorte zu analysieren. Das univariate konkurrierende Risikomodell zeigte, dass die prädiktiven Faktoren für CSS Geschlecht, Alter, Rasse, Familienstand, AJCC-Staging, TNM-Staging, Tumorgröße, LNR-Klassifikation, LODDS-Klassifikation, CEA-Niveau, ob der Patient eine Strahlen- oder Chemotherapie erhielt, und die Lokalisation des Primärtumors umfassten. Schließlich wurden die multivariate konkurrierende Risikoanalyse, das T-Staging, das N-Staging, das M-Staging, die LODDS-Klassifikation und die Lokalisation des Primärtumors als fünf unabhängige prognostische Marker für kolorektale SRCC-Patienten identifiziert. Die Ergebnisse univariater und multivariater konkurrierender Risikoanalysen sind in Tabelle 5 dargestellt, und die entsprechenden kurven der kumulativen Inzidenzfunktion (CIF) für die unabhängigen Risikofaktoren sind in Abbildung 5 dargestellt. Basierend auf den fünf signifikanten Variablen (T-Staging, N-Staging, M-Staging, LODDS-Klassifikation und die Lokalisation des Primärtumors) haben wir ein prognostisches Nomogramm entwickelt (Abbildung 6A). Wir stellten fest, dass LODDS im Vergleich zu pN ein höheres Gewicht aufwies. Dieses Ergebnis stimmt mit den vorherigen Ergebnissen überein und deutet darauf hin, dass das LODDS-System das beste System zur Beurteilung des LN-Status bei SRCC-Patienten ist.
Um die Genauigkeit des Modells zu beurteilen, haben wir Kalibrierungskurven erstellt (Abbildungen 6B-D). Die Ergebnisse zeigten, dass das Modell bei der Vorhersage des Gesamtüberlebens von Patienten nach 1, 3 und 5 Jahren gut abschneidet. Die Anpassung der Kurven an die 45°-Linie zeigt eine starke Konsistenz des Modells. Die Auswertungsergebnisse der ROC-Kurve für das Nomogramm (Abbildungen 5E-G) zeigten, dass die Fläche unter der Kurve (AUC) für Vorhersagen nach 1, 3 und 5 Jahren größer als 0,75 war. Diese Ergebnisse deuten darauf hin, dass die Vorhersagekurven für 3 und 5 Jahre signifikante Vorteile zeigten, was darauf hindeutet, dass das Nomogramm wertvolle klinische Anwendungen und einen Referenzwert hat.

Abbildung 1: Flussdiagramm, das den Screening-Prozess in der SEER-Datenbank darstellt. Durch unsere Ein- und Ausschlusskriterien konnten wir erfolgreich Darmkrebspatienten aus der SEER-Datenbank für eine nachfolgende Analyseserie auf Basis von R auswählen. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Abbildung 2: Assoziation von LNR-, LODDS- und pN-Staging mit CSS in der Trainingskohorte. Diese Abbildung veranschaulicht die Ergebnisse der multivariaten Cox-Regressionsanalyse für (A) LNR, (B) LODDS und (C) pN-Staging, die zusammen mit anderen unabhängigen prognostischen Faktoren ausgewertet wurden. Die Analyse umfasst Hazard Ratios (HR) und 95 % Konfidenzintervalle (CI). Die Ergebnisse zeigen, dass LNR, LODDS und pN-Status signifikante prognostische Faktoren für das krebsspezifische Überleben bei Patienten mit SRCC sind, wobei alle HR-Werte eine statistische Signifikanz aufweisen (p < 0,05). *p < 0,05, **p < 0,01, ***p < 0,001. Fehlerbalken stellen ein KI von 95 % dar. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Abbildung 3: Relative Bedeutung von Variablen. (A) XGBoost-Modell, (B) RF-Modell und (C) NN-Modell. Diese Abbildung bewertet die relative Bedeutung von Variablen. In den Modellen XGBoost und RF hatte LNR die höchste Bedeutung, wobei LODDS ebenfalls eine beträchtliche Bedeutung hatte. Umgekehrt zeigte LODDS im NN-Modell eine überlegene Vorhersagefähigkeit im Vergleich zu pN und LNR. Basierend auf den kombinierten Ergebnissen der drei Modelle wird das LODDS-System als das effektivste für die Beurteilung des LN-Status bei SRCC-Patienten angesehen. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Abbildung 4: ROC-Kurven und Kalibrierungskurven der ML-Modelle, XGBoost und eXtreme Gradient Boosting. (A, D) die Trainingskohorte, (B, E) die Validierungskohorte und (C, F) die externe Validierungskohorte. Der Wert für die Fläche unter der Kurve (AUC), der näher an 1 liegt, gibt eine bessere Klassifizierungsleistung des Modells an. Die Fehlerbalken stellen das 95 %-Konfidenzintervall für die vorhergesagte Wahrscheinlichkeit des Eintretens des tatsächlichen Ereignisses dar. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
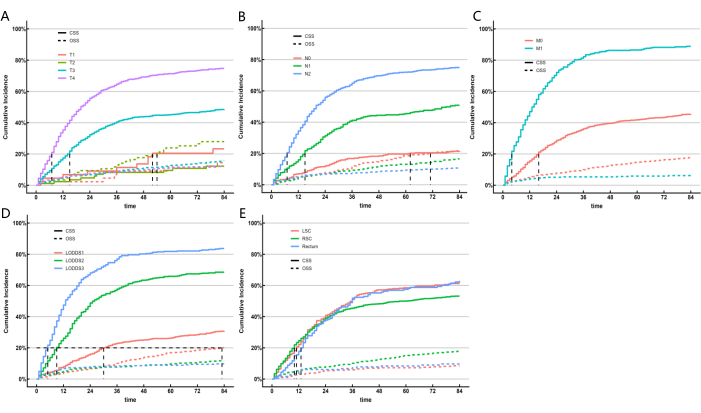
Abbildung 5: Kumulative Inzidenzschätzungen des Todes nach Patientenmerkmalen bei kolorektaler SRCC. CIF von Untergruppen. Der Gray-Test wurde angewendet. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
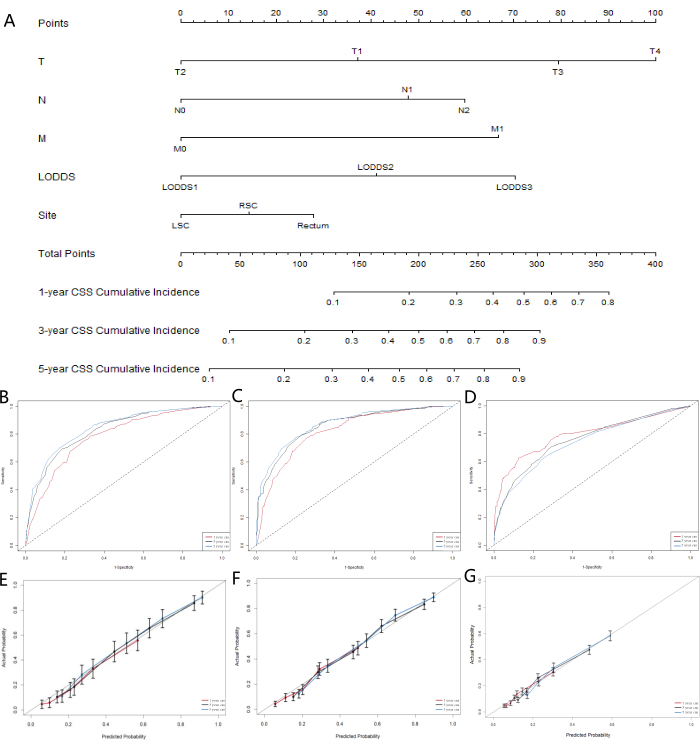
Abbildung 6: Entwicklung und Validierung von Nomogrammen für CSS bei kolorektalen SRCC-Patienten. (A) Ein konkurrierendes Risiko-Nomogramm, das die 1-Jahres-, 3-Jahres- und 5-Jahres-krebsspezifische Überlebenswahrscheinlichkeit von Patienten mit kolorektaler SRCC vorhersagt. Die Kalibrierungskurven der Nomogramme zur Vorhersage des 1-, 3- und 5-Jahres-krebsspezifischen Überlebens in der (B) Trainingskohorte, (C) Validierungskohorte und (D) externen Validierungskohorte. Empfänger-Funktionskennlinien zur Vorhersage des 1-, 3- und 5-Jahres-krebsspezifischen Überlebens in der (E)-Trainingskohorte, der (F)-Validierungskohorte und der (G) externen Validierungskohorte. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Tabelle 1: Klinische Merkmale von Patienten mit kolorektaler SRCC. Bitte klicken Sie hier, um diese Tabelle herunterzuladen.
Tabelle 2: Univariate Cox-Regressionsanalyse von CSS in der Trainingskohorte. Bitte klicken Sie hier, um diese Tabelle herunterzuladen.
Tabelle 3: Vorhersageleistung der drei Lymphknoten-Staging-Systeme. Bitte klicken Sie hier, um diese Tabelle herunterzuladen.
Tabelle 4: Prädiktive Leistung der Modelle in der Validierungskohorte und in den externen Validierungskohorten. Bitte klicken Sie hier, um diese Tabelle herunterzuladen.
Tabelle 5: Univariate und multivariate konkurrierende Risikoanalyse für die krebsspezifische Mortalität von kolorektalem SRCC in der Trainingskohorte. Bitte klicken Sie hier, um diese Tabelle herunterzuladen.
Diskussion
Darmkrebs (CRC) SRCC ist eine seltene und spezielle Unterform des Darmkrebses mit schlechter Prognose. Daher muss der Prognose von SRCC-Patienten größere Aufmerksamkeit geschenkt werden. Eine genaue Überlebensvorhersage für SRCC-Patienten ist entscheidend, um ihre Prognose zu bestimmen und individuelle Behandlungsentscheidungen zu treffen. In dieser Studie untersuchten wir den Zusammenhang zwischen klinischen Merkmalen und Prognose bei SRCC-Patienten und identifizierten das optimale LN-Staging-System für SRCC-Patienten aus der SEER-Datenbank. Unseres Wissens ist dies die erste Studie, die das geeignete LN-System für kolorektale SRCC-Patienten durch einen umfassenden Einsatz von maschinellem Lernen und konkurrierenden Risikoanalysemethoden ermittelt und ein Nomogramm zur prognostischen Vorhersage konstruiert.
Die Anzahl der metastasierten LNs bei Darmkrebspatienten ist ein wichtiger Indikator für die Prognose und das Rezidiv. Ein genaues LN-Staging spielt eine Schlüsselrolle bei der Bestimmung von Behandlungsstrategien und Prognosen für SRCC-Patienten. LNR und LODDS sind alternative Methoden, die verwendet werden, um die Beteiligung von LN an GC zu bewerten, Staging-Systeme zu verbessern und genauere prognostische Informationen zu liefern10,13. Wir haben die Korrelation zwischen LODDS, LNR und pN-Staging mit CSS bei SRCC-Patienten unter Verwendung der SEER-Datenbank aufgedeckt. Die Vorhersagefähigkeiten dieser drei LN-Systeme (LNR, LODDS und pN) wurden anhand von AUCs, AICs, BICs und C-Indizes verglichen. Die Unterschiede zwischen ihnen waren jedoch minimal. Aus diesem Grund haben wir drei Methoden des maschinellen Lernens – Xgboost, RF und NN – verwendet, um die wichtigsten Merkmale als optimales LN-System auszuwählen. Basierend auf den kombinierten Ergebnissen der drei Methoden haben wir LODDS als das geeignete LN-System definiert.
OSS ist jedoch ein konkurrierendes Risikoereignis, das die Prognose von CSS-Patienten beeinflusst. Bei der Überprüfung von Variablen für die Aufnahme in das Modell des maschinellen Lernens mit der Cox-Regressionsmethode wurden die Auswirkungen von OSS nicht berücksichtigt, was zu einer ungenauen Bewertung der Risikokennzahlen führen kann12. Um das optimale LN-Bewertungssystem für SRCC-Patienten weiter zu bestimmen, haben wir daher ein konkurrierendes Risikomodell erstellt. Die Ergebnisse bestätigten erneut, dass das LODDS-Staging-System im Vergleich zum pN-System genauere prognostische Informationen liefert. Während der Nachbeobachtung starben von 2409 Patienten 1339 (56%) an CSS und 464 (19%) an OSS. Darüber hinaus haben wir auch ein konkurrierendes Risikodiagramm entwickelt, um die krebsspezifischen Mortalitätsraten nach 1 Jahr, 3 Jahren und 5 Jahren vorherzusagen. Wir glauben, dass dieses Modell erhebliche Auswirkungen auf die klinische Forschung mit kolorektalen SRCC-Patienten hat. Obwohl das American Joint Committee on Cancer das TNM-System als Staging-System für alle histologischen Arten von Darmkrebs empfiehlt, wird es hauptsächlich für das Staging des kolorektalen Adenokarzinoms verwendet. Die AJCC N-Stufe ist durch TLN begrenzt, während LNR die Auswirkungen von NLN 13,14,15,16 nicht berücksichtigt. Berichte deuten darauf hin, dass LODDS weniger von TLN betroffen ist und die Anzahl der NLN10,17 berücksichtigt. Scarinci et al. zeigten, dass LODDS das OS bei Darmkrebspatienten besser vorhersagt als LNR- und pN-Staging und schlugen vor, dass zukünftige Forschungen seine Rolle bei verschiedenen Darmkrebs-Subtypen validieren sollten18. In dieser Studie fanden wir heraus, dass LODDS einen signifikanten prognostischen prädiktiven Effekt auf CSS bei kolorektaler SRCC hat. Daher kann LODDS ein wertvolles Instrument zur Beurteilung der Lymphknotendissektion und der Prognose bei kolorektalen SRCC-Patienten sein. Obwohl noch kein optimaler Schwellenwert für LODDS festgelegt wurde, hat es sich als das zuverlässigste LN-Bereitstellungssystem erwiesen. Mit zunehmender Aufmerksamkeit für LODDS wird allgemein angenommen, dass es in absehbarer Zeit eine breite Anerkennung im klinischen Umfeld finden wird.
Unsere Studie ergab, dass die Lokalisation des Primärtumors ein wichtiger prädiktiver Faktor für CSS ist, mit einer signifikant schlechteren Prognose für rektale SRCC, was mit früheren Studien übereinstimmt 12,19,20. Rektale SRCC kann einzigartige klinische, pathologische und molekulare Merkmale aufweisen21,22, die weitere Untersuchungen rechtfertigen. Die aus den Vorhersagemodellen abgeleiteten Diagramme sind wichtige und effektive Werkzeuge für die klinische Entscheidungsfindung und Patientenberatung. Unseres Wissens ist diese Studie die erste, die ML-Modelle und konkurrierende Risikomodelle integriert, um das optimale LN-Staging-System für SRCC-Patienten zu untersuchen. Wir haben drei ML-Modelle entwickelt und validiert, um die Prognose von SRCC-Patienten vorherzusagen. Im Testdatensatz zeigten XGBoost-, RF- und NN-Modelle eine gute prognostische Vorhersageleistung auf der Grundlage von AUC-Werten und entsprechenden Metriken. So können ML-Modelle bei Behandlungsentscheidungen für SRCC-Patienten helfen, indem sie die Prognose vorhersagen. Darüber hinaus haben wir konkurrierende Risikodiagramme auf der Grundlage proportionaler Gefahrenmodelle erstellt, um prädiktive Faktoren für kolorektale SRCC zu analysieren und die Rolle von LODDS darin zu bewerten. Wir verwendeten den C-Index und die Kalibrierungskurve, um die Vorhersageleistung des Nomogramms zu bewerten. Das Diagramm zeigte gemeinsame klinische Variablen, wie z. B. die primäre Tumorlokalisation und die LODDS-Gruppierung. Darüber hinaus ist das von uns erstellte Nomogramm eine effektive Methode zur Vorhersage des 1-Jahres-, 3-Jahres- und 5-Jahres-CSS bei kolorektalen SRCC-Patienten. Dieses Tool kann Ärzten dabei helfen, genaue, gründliche und zeitnahe prognostische Bewertungen für jeden kolorektalen SRCC-Patienten durchzuführen, und ermöglicht es ihnen, personalisierte Behandlungspläne zu formulieren23.
Schließlich weist diese Studie mehrere Einschränkungen auf. Zunächst wurden die Patienten in der Studie zwischen 2004 und 2015 diagnostiziert, was zu einer relativ kurzen Nachbeobachtungszeit führte. Wir gehen davon aus, dass ein längerer Nachbeobachtungszeitraum dazu beitragen würde, die Genauigkeit der Modellvorhersagen zu verbessern. Zweitens ist das hier verwendete Studiendesign retrospektiv und stützt sich auf Daten aus der SEER-Datenbank, was zu einigen inhärenten Verzerrungen führen kann. Einige Informationen, wie z. B. die Position von metastasierten LNs, wurden nicht aufgezeichnet. Schließlich war die Mehrheit der Patienten in dieser Studie weiß, was breitere Studien mit verschiedenen Populationen erforderlich machte, um diese Ergebnisse zu bestätigen und zu verstärken.
Schlussfolgerung
Die Studie ergab, dass das LODDS eine starke prognostische Vorhersagefähigkeit für kolorektale SRCC aufweist. Aufbauend auf dieser Grundlage haben wir ein Nomogramm entwickelt, das auf einem konkurrierenden Risikomodell basiert, um die Gesamtüberlebensraten in Intervallen von 1 Jahr, 3 Jahren und 5 Jahren für kolorektale SRCC-Patienten vorherzusagen. Nach einer Reihe von Bewertungen und internen Validierungen hat das Nomogramm eine signifikante klinische Anwendbarkeit und einen signifikanten Wert bewiesen und bietet Ärzten eine Orientierungshilfe bei der Entscheidungsfindung bei der Behandlung. Zusätzlich haben wir drei ML-Modelle konstruiert. Diese ML-Ansätze haben das Potenzial, die prognostischen Vorhersagefähigkeiten von SRCC zu verbessern und Ärzten dabei zu helfen, zu verstehen, wie ML zur Optimierung von Behandlungs- und Nachsorgestrategien eingesetzt werden kann.
Offenlegungen
Die Autoren haben keine finanziellen Interessenkonflikte offenzulegen.
Danksagungen
Nichts
Materialien
| Name | Company | Catalog Number | Comments |
| SEER database | National Cancer institiute at NIH | ||
| X-tile software | Yale school of medicine | ||
| R-studio | Posit |
Referenzen
- Siegel, R. L., Giaquinto, A. N., Jemal, A. Cancer statistics, 2024. CA Cancer J Clin. 74 (1), 12-49 (2024).
- Korphaisarn, K., et al. Signet ring cell colorectal cancer: Genomic insights into a rare subpopulation of colorectal adenocarcinoma. Br J Cancer. 121 (6), 505-510 (2019).
- Willauer, A. N., et al. Clinical and molecular characterization of early-onset colorectal cancer. Cancer. 125 (12), 2002-2010 (2019).
- Watanabe, A., et al. A case of primary colonic signet ring cell carcinoma in a young man which preoperatively mimicked Phlebosclerotic colitis. Acta Med Okayama. 73 (4), 361-365 (2019).
- Kim, H., Kim, B. H., Lee, D., Shin, E. Genomic alterations in signet ring and mucinous patterned colorectal carcinoma. Pathol Res Pract. 215 (10), 152566(2019).
- Deng, X., et al. Neoadjuvant radiotherapy versus surgery alone for stage II/III mid-low rectal cancer with or without high-risk factors: A prospective multicenter stratified randomized trial. Ann Surg. 272 (6), 1060-1069 (2020).
- Buk Cardoso, L., et al. Machine learning for predicting survival of colorectal cancer patients. Sci Rep. 13 (1), 8874(2023).
- Monterrubio-Gómez, K., Constantine-Cooke, N., Vallejos, C. A. A review on statistical and machine learning competing risks methods. Biom J. 66 (2), e2300060(2024).
- Kim, H. J., Choi, G. S. Clinical implications of lymph node metastasis in colorectal cancer: Current status and future perspectives. Ann Coloproctol. 35 (3), 109-117 (2019).
- Xu, T., et al. Log odds of positive lymph nodes is an excellent prognostic factor for patients with rectal cancer after neoadjuvant chemoradiotherapy. Ann Transl Med. 9 (8), 637(2021).
- Chen, Y. R., et al. Prognostic performance of different lymph node classification systems in young gastric cancer. J Gastrointest Oncol. 12 (4), 285-1300 (2021).
- Bouvier, A. M., et al. How many nodes must be examined to accurately stage gastric carcinomas? Results from a population based study. Cancer. 94 (11), 2862-2866 (2002).
- Coburn, N. G., Swallow, C. J., Kiss, A., Law, C. Significant regional variation in adequacy of lymph node assessment and survival in gastric cancer. Cancer. 107 (9), 2143-2151 (2006).
- Li Destri, G., Di Carlo, I., Scilletta, R., Scilletta, B., Puleo, S. Colorectal cancer and lymph nodes: the obsession with the number 12. World J Gastroenterol. 20 (8), 1951-1960 (2014).
- Dinaux, A. M., et al. Outcomes of persistent lymph node involvement after neoadjuvant therapy for stage III rectal cancer. Surgery. 163 (4), 784-788 (2018).
- Sun, Y., Zhang, Y., Huang, Z., Chi, P. Prognostic implication of negative lymph node count in ypN+ rectal cancer after neoadjuvant chemoradiotherapy and construction of a prediction nomogram. J Gastrointest Surg. 23 (5), 1006-1014 (2019).
- Xu, Z., Jing, J., Ma, G. Development and validation of prognostic nomogram based on log odds of positive lymph nodes for patients with gastric signet ring cell carcinoma. Chin J Cancer Res. 32 (6), 778-793 (2020).
- Scarinci, A., et al. The impact of log odds of positive lymph nodes (LODDS) in colon and rectal cancer patient stratification: a single-center analysis of 323 patients. Updates Surg. 70 (1), 23-31 (2018).
- Nitsche, U., et al. Prognosis of mucinous and signet-ring cell colorectal cancer in a population-based cohort. J Cancer Res Clin Oncol. 142 (11), 2357-2366 (2016).
- Kang, H., O'Connell, J. B., Maggard, M. A., Sack, J., Ko, C. Y. A 10-year outcomes evaluation of mucinous and signet-ring cell carcinoma of the colon and rectum. Dis Colon Rectum. 48 (6), 1161-1168 (2005).
- Sung, C. O., et al. Clinical significance of signet ring cells in colorectal mucinous adenocarcinoma. Mod Pathol. 21 (12), 1533-1541 (2008).
- Alvi, M. A., et al. Molecular profiling of signet ring cell colorectal cancer provides a strong rationale for genomic targeted and immune checkpoint inhibitor therapies. Br J Cancer. 117 (2), 203-209 (2017).
- Brownlee, S., et al. Evidence for overuse of medical services around the world. Lancet. 390 (10090), 156-168 (2017).
Nachdrucke und Genehmigungen
Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden
Genehmigung beantragenThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten