Circuitos RC/RL/LC

Fonte: Yong P. Chen, PhD, Departamento de Física & Astronomia, Faculdade de Ciências, Universidade purdue, West Lafayette, IN

Capacitores (C), indutores (L) e resistores (R) são cada um elemento importante do circuito com comportamentos distintos. Um resistor dissipa energia e obedece à lei de Ohm, com sua tensão proporcional à sua corrente. Um capacitor armazena energia elétrica, com sua corrente proporcional à taxa de mudança de sua tensão, enquanto um indutor armazena energia magnética, com sua tensão proporcional à taxa de mudança de sua corrente. Quando esses elementos de circuito são combinados, eles podem fazer com que a corrente ou tensão varie com o tempo de várias maneiras interessantes. Essas combinações são comumente usadas para processar sinais elétricos dependentes de tempo ou frequência, como em circuitos de corrente alternada (AC), rádios e filtros elétricos. Este experimento demonstrará os comportamentos dependentes do tempo dos circuitos resistor-capacitor(RC), indutor de resistor (RL) e capacitor indutor (LC). O experimento demonstrará os comportamentos transitórios dos circuitos RC e RL usando uma lâmpada (resistor) conectada em série a um capacitor ou indutor, ao conectar (e ligar) uma fonte de alimentação. O experimento também demonstrará o comportamento oscilatório de um circuito LC.

Considere um resistor (com resistência R) em série de um capacitor (com capacitância C), conectado a uma fonte de tensão (com saída de tensão V), como retratado na Figura 1. Se a fonte de tensão estiver ligada no tempo t = 0, uma corrente dependente do tempo i(t) começará a fluir no circuito, através do resistor R. Esta corrente também é conhecida como a "corrente de carregamento" para o capacitor, pois "flui para dentro" do capacitor (ou seja,traz cargas opostas às placas opostas no capacitor) para desenvolver uma queda de tensão dependente do tempo V_c através do capacitor. Uma vez que a tensão total V da fonte de tensão é compartilhada entre a queda de tensão através do resistor (que é i×R) e que através do capacitor (V_C):

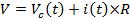(Equação 1)

No início (t = 0, imediatamente após a fonte de tensão ser ligada com saída V), o capacitor não teve a chance de desenvolver qualquer tensão e, portanto, V_C(t = 0) = 0, e (de acordo com a Equação 1), i(t = 0) = V/R. À medida que o tempo avança, os encargos aumentam sobre o capacitor e V_c aumentarão, e assim i(t) diminuirá. Além disso, essas acusações tendem a repelir encargos adicionais que chegam ao capacitor (ou seja,se opõem ao processo de cobrança). Após um tempo suficiente, este processo de carregamento pára e, portanto, i(t→∞) = 0 e V_c(t→) = V. Isso significa que o capacitor agora está totalmente carregado (ou tem a tensão completa V da fonte de tensão caindo através dele), sem mais fluxos de corrente, e o capacitor se comporta como um interruptor aberto neste estado totalmente carregado e estável. Em geral, um capacitor conduz mais para maior frequência ou corrente transitória, enquanto conduz menos ou não para menor frequência ou corrente de estado estável (DC).

A corrente completa e quantitativa dependente do tempo i(t)pode ser resolvida por:

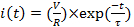(Equação 2)

onde

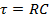  (Equação 3)

é conhecida como a "constante de tempo RC" para o circuito "RC" e caracteriza em geral a escala de tempo para a resposta do circuito RC (aqui a mudança na corrente) sobre uma mudança transitória em uma entrada (aqui o desligamento da fonte de tensão). Tal corrente dependente do tempo dada pela Equação 2 é retratada na Figura 1.

Neste caso, o tempo rc também representa a escala de tempo característica para carregar o capacitor. É a escala de tempo para descarregar um capacitor, ou seja, se um capacitor totalmente carregado (com tensão V) estiver diretamente conectado a um resistor para formar um circuito fechado (correspondente à substituição da fonte de tensão na Figura 1 por um fio curto), então a corrente que flui através do resistor seguirá novamente a Equação 2.

Uma análise análoga pode ser feita para um resistor em série de um indutor, ou um circuito "RL", como o mostrado na Figura 2. No entanto, o comportamento de um indutor é oposto ao de um capacitor, no sentido de que o indutor conduz melhor em menor frequência (para corrente de estado constante o indutor age como um fio curto com pouca resistência), mas conduz muito menos em maior frequência ou em uma situação transitória (porque um indutor sempre tenta se opor à mudança em sua corrente). Como resultado, a corrente i(t) que fluiria no circuito RL mostrada na Figura 2 após o fechamento do interruptor no momento t = 0 (ou ligar a fonte de tensão para saída de V) seria:

(Equação 4)

onde

(Equação 5)

que é a escala de tempo característica geral para a resposta (aqui a mudança na corrente) do circuito RL sobre uma mudança transitória em uma entrada (aqui o interruptor da fonte de tensão). Note aqui, i(t = 0) = 0, porque inicialmente a corrente através do indutor (que é a mesma corrente através do resistor) não teve a chance de mudar de seu valor zero inicial (antes que a fonte de tensão seja ligada), e o indutor tenta se opor a qualquer mudança repentina em sua corrente. Depois que o circuito atinge seu estado estável, a corrente não está mais mudando com o tempo, então o indutor se comporta como um fio curto, e de fato i(t→∞) = V/R de acordo com a Equação 4. Este comportamento (a corrente aumenta a partir de 0 e se aproxima de V/R exponencialmente) é retratado na Figura 2, e note que é oposto do comportamento para o circuito RC (Equação 2 e Figura 1, onde a corrente diminui de V/R e decai para 0 exponencialmente).

A dependência de tempo exponencial no circuito RC ou RL está relacionada com a natureza dissipativa do resistor. Em contraste, um circuito "LC" onde um capacitor está diretamente conectado a um indutor com resistências insignificantes, como o mostrado na Figura 3a,exibiria um comportamento oscilante ou "ressonante". A Figura 3a retrata um capacitor, inicialmente carregado para ter uma queda de tensão V, conectado a um indutor (sem corrente através dele inicialmente) no momento t = 0. Pode-se mostrar que a tensão subsequente no capacitor (mesmo no indutor) teria a seguinte dependência de tempo oscilativa (sinusoidal):

(Equação 6)

onde

(Equação 7)

é a "frequência de oscilação" ou "frequência ressonante" (aqui, a frequência refere-se à frequência angular) do circuito LC. A corrente através do indutor é:

(Equação 8)

O capacitor primeiro descarrega através do indutor (V_C(t) diminui e i(t) aumenta. Quando ωt atinge π/2, o capacitor é totalmente descarregado (V_C = 0) e a corrente máxima flui no indutor. Em seguida, o capacitor é carregado novamente (pela corrente que flui no indutor) na polaridade reversa (V_C(t) atinge -V quando ωt atinge π), e então descarrega novamente (totalmente descarregado quando ωt atinge 3π/2) e recarrega à polaridade original de V_C = V quando ωt atinge 2π. O ciclo se repete com o período no tempo(t)de,

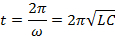
Tal comportamento oscilatório, retratado na Figura 3b,também corresponde ao capacitor e indutor trocando energia eletromagnética entre si (um capacitor armazena energia no campo elétrico devido à queda de tensão, e um indutor armazena energia no campo magnético devido à correnteza). Na situação ideal sem resistência (e, portanto, sem dissipação) no circuito, a oscilação pode continuar indefinidamente. Na presença de alguma resistência (dissipação), por exemplo, no circuito mostrado na Figura 3c, também conhecido como circuito "RLC", tal oscilação será amortecida (se não houver fonte de alimentação externa), retratada na Figura 3d, e depois de um tempo suficiente tanto a tensão quanto a corrente chegariam a zero.

Figura 1: Diagrama mostrando um circuito RC, com um resistor (R) em série com um capacitor (C), conectado a uma fonte de tensão com um interruptor. Uma corrente de tempo representativa dependente (dada pela Equação 2) é retratada acima da figura.

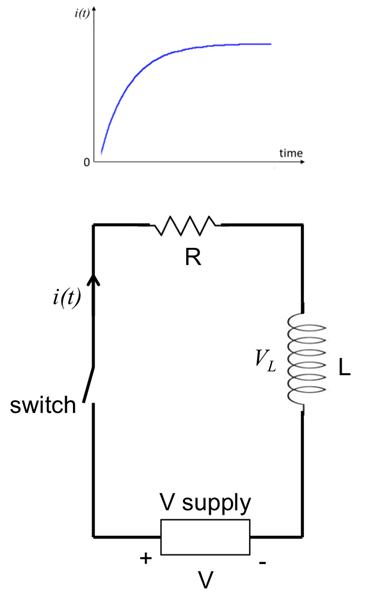
Figura 2: Diagrama mostrando um circuito RL, com um resistor (R) em série com um indutor (L), conectado a uma fonte de tensão com um interruptor. Uma corrente de tempo representativa (dada pela Equação 4) é retratada acima da figura.

Figura 3: (a) Diagrama mostrando um circuito LC, com um indutor (L) conectado com um capacitor (C) em um circuito fechado. (b) Uma tensão de tempo representativa dependente do capacitor, mostrando oscilação não diminuída (dada pela Equação 6). (c) Diagrama mostrando um circuito LC com uma resistência série (R), também conhecido como circuito RLC. (d) Uma tensão de tempo representativa dependente do capacitor para o circuito mostrado em (c), mostrando uma oscilação amortecido.

1. Usando um osciloscópio

1. Obtenha um osciloscópio, uma pequena lâmpada (com resistência R de alguns Ω), um interruptor e uma fonte de tensão DC (ou, alternativamente, uma bateria de 1,5 V).
2. Conecte o circuito conforme mostrado na Figura 4,com o interruptor aberto. As conexões neste experimento podem ser feitas com cabos, grampos ou plugues de banana nas portas receptoras dos instrumentos.
3. Selecione a escala vertical do osciloscópio para um intervalo próximo a 1 V. Selecione a escala de tempo do osciloscópio para um intervalo próximo a 1 s.
4. Feche o interruptor (ligando assim a lâmpada). Observe a lâmpada, bem como o traço ("forma de onda") na tela do osciloscópio. O osciloscópio, conectado paralelamente à lâmpada, medirá a tensão através da lâmpada, e essa tensão é proporcional à corrente através da lâmpada.
5. Agora abra novamente o interruptor (desligando assim a lâmpada). Observe novamente a lâmpada, bem como o traço ("forma de onda") na tela do osciloscópio.
6. Repita as etapas 1.4 e 1.5, se necessário.

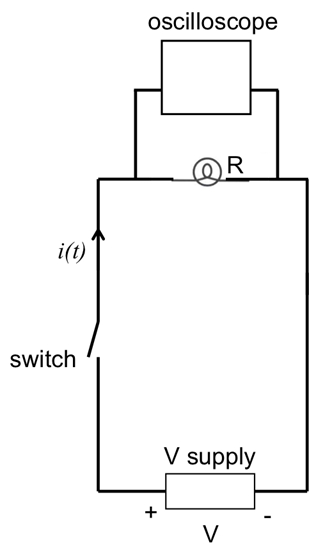
Figura 4: Diagrama mostrando uma lâmpada conectada a um suprimento de tensão com um interruptor. Um osciloscópio é conectado em paralelo com a lâmpada para medir sua tensão (proporcional à corrente).

2. Circuito RL

1. Obtenha um indutor com indutância L de 1 milihenry (mH).
2. Conecte o indutor em série à lâmpada (com o osciloscópio conectado em paralelo à lâmpada) e ao fornecimento de tensão com um interruptor aberto, como mostrado na Figura 5a.
3. Feche o interruptor. Observe a lâmpada, bem como a forma de onda no osciloscópio.
4. Abra o interruptor. Obtenha outra lâmpada (do mesmo tipo da primeira lâmpada) e conecte-a em paralelo com a primeira lâmpada, como mostrado na Figura 5b.
5. Repita o passo 2.3 (feche o interruptor) e observe as lâmpadas e o osciloscópio.

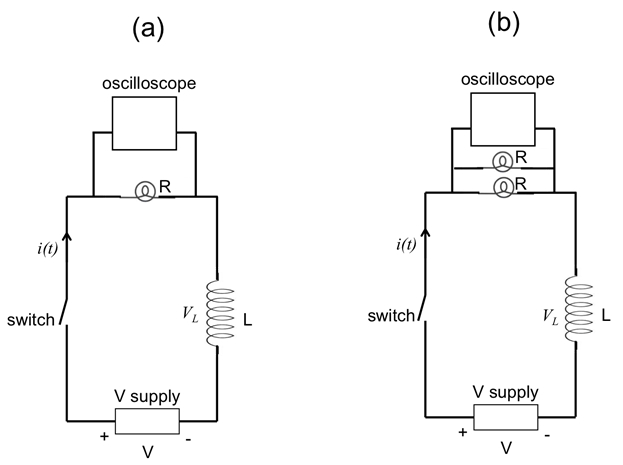
Figura 5: Diagrama mostrando um circuito RL, com uma lâmpada ( a) ou duas lâmpadas paralelas (b) agindo como o resistor (R). Um osciloscópio é conectado em paralelo com a lâmpada para medir a tensão através da lâmpada, proporcional à corrente total.

3. Circuito RC

1. Obter um capacitor com capacitância de 1 Farad (F).
2. Conecte o capacitor em série com a lâmpada (que está conectada paralelamente ao osciloscópio) e, juntamente, ao fornecimento de tensão com o interruptor aberto, conforme mostrado na Figura 6a. Isso corresponde ao circuito similar mostrado na Figura 5a conectado na etapa 2.2, exceto com o indutor substituído pelo capacitor.
3. Feche o interruptor. Observe a lâmpada, bem como a forma de onda no osciloscópio.
4. Abra o interruptor. Conecte a segunda lâmpada em paralelo com a primeira lâmpada, como mostrado na Figura 6b.
5. Repita o passo 3.3 (feche o interruptor) e observe as lâmpadas e o osciloscópio.

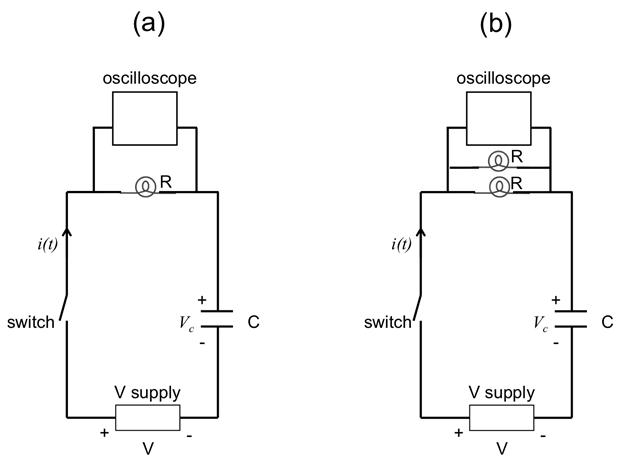
Figura 6: Diagrama mostrando um circuito RC, com uma lâmpada ( a) ou duas lâmpadas paralelas (b) agindo como o resistor (R). Um osciloscópio é conectado em paralelo com a lâmpada para medir a tensão através da lâmpada, proporcional à corrente total.

3. Circuito LC

1. Conecte um indutor de 8 mH em série com outro interruptor aberto (switch #2) e, em paralelo, a um capacitor de 10 μF, como mostrado na Figura 7. Feche o interruptor #1 para ter o capacitor carregado. Nenhuma lâmpada é usada nesta parte do experimento.
2. Conecte o osciloscópio em paralelo com o capacitor, como mostrado na Figura 7.
3. Agora abra o interruptor #1, e logo imediatamente também feche o interruptor #2. Observe o osciloscópio.

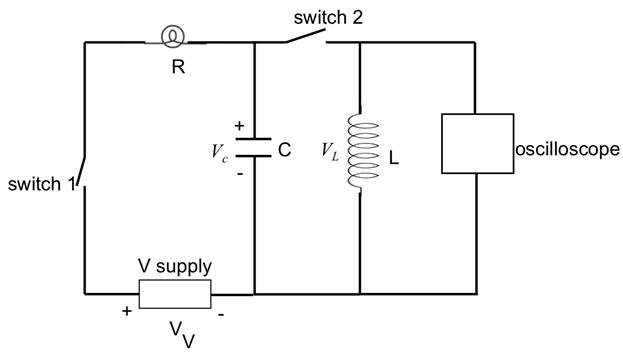
Figura 7: Diagrama mostrando um indutor (L) com um interruptor conectado em paralelo a um capacitor (C), que faz parte de um circuito RC da série estudado na Figura 6. O osciloscópio está agora conectado em paralelo ao indutor para medir sua tensão.

Para o passo 1, a lâmpada ligará e desligará "instantaneamente" ao fechar (etapa 1.4) e abrir (na etapa 1.5) o interruptor. Traços de osciloscópios representativos são mostrados na Figura 8.

Para o passo 2.3, após o fechamento do interruptor, pode-se observar que leva um pequeno, mas perceptível período de tempo para a lâmpada acender (em vez de instantaneamente como no passo 1). Quando duas lâmpadas paralelas são usadas (passo 2.5), leva mais tempo para as lâmpadas acenderem em comparação com a caixa anterior (etapa 2.3). Isso ocorre porque as duas lâmpadas paralelas dão uma resistência menor (R), e, portanto, uma constante de tempo mais longa τ_L = L/R para um circuito RL (note que a constante de tempo pode não ser exatamente o dobro do tempo porque as duas lâmpadas podem não ter exatamente as mesmas resistências, e pode haver outras resistências não desprezíveis no circuito). Traços representativos no osciloscópio para os dois casos são mostrados na Figura 9. A escala de tempo "ligar" medida no osciloscópio é ~ ms e é consistente com a constante de tempo esperada τ_L com base nos valores de indutância e resistência à lâmpada.

Para o passo 3.3, após o fechamento do interruptor, pode-se observar que a lâmpada brilhará brevemente antes de morrer. Quando duas lâmpadas paralelas são usadas (passo 3.5), leva um tempo menor para as lâmpadas morrerem em comparação com a caixa anterior (etapa 3.3). Isso ocorre porque as duas lâmpadas paralelas dão uma resistência menor (R), e, portanto, uma constante de tempo RC mais curta τ = RC. Traços representativos no osciloscópio para os dois casos são mostrados na Figura 10. A escala de tempo "ligar" de ~1 s é consistente com a constante de tempo esperada com base nos valores de capacitância e resistência à lâmpada.

Para a etapa 4.3, uma tensão oscilatória como as retratadas na Figura 3b, 3d pode ser observada no osciloscópio. Alguns amortecimentos da oscilação podem ser observados devido à resistência finita dos fios que ligam o circuito. O período de oscilação, na ordem do milissegundo, é consistente com o período de oscilação da LC esperado (2π ) com base nos valores de capacitância e resistência.

Figura 8: Traços de osciloscópio representativos (ou "formas de onda") que podem ser observados no experimento retratado na Figura 4, quando o interruptor é fechado ou aberto, medindo a tensão através de uma lâmpada diretamente ligada a uma fonte de tensão.

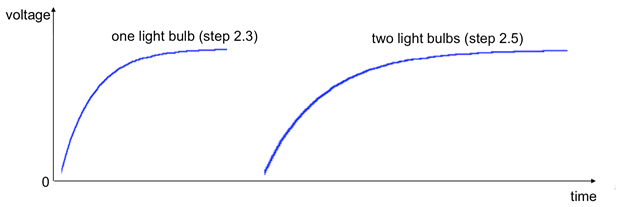
Figura 9: Traços de osciloscópio representativos (ou "formas de onda") que podem ser observados quando o interruptor é fechado no experimento retratado na Figura 5, medindo a tensão através de uma lâmpada conectada em série de um indutor e uma fonte de tensão.

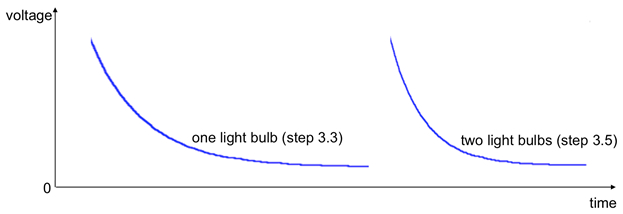
Figura 10: Traços de osciloscópio representativos (ou "formas de onda") que podem ser observados quando o interruptor é fechado no experimento retratado na Figura 6, medindo a tensão através de uma lâmpada conectada em série de um capacitor e uma fonte de tensão

Neste experimento, demonstramos a resposta dependente do tempo (liga e desliga exponencial) em circuitos RC ou RL, e como a mudança da resistência afeta a constante de tempo. Também demonstramos a resposta oscilatória em um circuito LC.

Os circuitos RC, RL e LC são blocos de construção essenciais em muitas aplicações de circuito. Por exemplo, circuitos RC e RL são comumente usados como filtros (aproveitando o fato de que os capacitores tendem a passar sinais de alta frequência, mas bloqueiam sinais de baixa frequência, enquanto o oposto é verdadeiro para indutores). Eles também são úteis para o processamento de sinal elétrico, por exemplo, tomando o derivado ou integral de um sinal elétrico. O circuito LC é um exemplo simples de um "oscilador" elétrico ou circuito de ressonância e é um componente comum em circuitos usados para amplificadores, sintonização de rádio, etc.

O autor do experimento reconhece a ajuda de Gary Hudson para a preparação do material e Chuanhsun Li por demonstrar os passos no vídeo.