Momento angular
Visión general
Fuente: Nicolás Timmons, Asantha Cooray, PhD, Departamento de física & Astronomía, Facultad de ciencias física, Universidad de California, Irvine, CA
El momento angular se define como el producto del momento de inercia y la velocidad angular del objeto. Como su análogo lineal, momento angular se conserva, lo que significa que el ímpetu angular total de un sistema no va a cambiar si hay no hay torques externos en el sistema. Un esfuerzo de torsión es el equivalente rotacional de una fuerza. Porque es un conservado, el ímpetu angular es una cantidad importante en la física.
El objetivo de este experimento es medir el ímpetu angular de una varilla giratoria y con la conservación del ímpetu angular para explicar dos manifestaciones rotacionales.
Principios
El momento angular se puede escribir como:
 , (Ecuación 1)
, (Ecuación 1)
donde  es el momento de inercia y
es el momento de inercia y  es la velocidad angular. El momento de inercia es el análogo rotacional de la masa para movimiento lineal. Se relaciona con la distribución en masa de un objeto giratorio y el eje de rotación. Cuanto mayor sea el momento de inercia, el par más es necesario para provocar una aceleración angular de un objeto. La regla de derecha puede utilizarse para determinar la dirección del momento angular. Cuando enrollamiento de los dedos de la mano derecha en el sentido de rotación, los puntos del dedo pulgar extendido en la dirección del momento angular.
es la velocidad angular. El momento de inercia es el análogo rotacional de la masa para movimiento lineal. Se relaciona con la distribución en masa de un objeto giratorio y el eje de rotación. Cuanto mayor sea el momento de inercia, el par más es necesario para provocar una aceleración angular de un objeto. La regla de derecha puede utilizarse para determinar la dirección del momento angular. Cuando enrollamiento de los dedos de la mano derecha en el sentido de rotación, los puntos del dedo pulgar extendido en la dirección del momento angular.
Un esfuerzo de torsión se define como el producto de una fuerza aplicada a cierta distancia de un eje de rotación:
 , (Ecuación 2)
, (Ecuación 2)
donde  es la fuerza aplicada y
es la fuerza aplicada y  es la distancia al eje de rotación. Si un esfuerzo de torsión actúa sobre un objeto, se cambiará la velocidad angular de ese objeto, junto a su ímpetu angular. Si la suma de los pares en un objeto es igual a cero, el ímpetu angular total se conserva y tendrá el mismo valor final como lo hizo inicialmente.
es la distancia al eje de rotación. Si un esfuerzo de torsión actúa sobre un objeto, se cambiará la velocidad angular de ese objeto, junto a su ímpetu angular. Si la suma de los pares en un objeto es igual a cero, el ímpetu angular total se conserva y tendrá el mismo valor final como lo hizo inicialmente.
Un divertido ejemplo de la conservación del ímpetu angular puede demostrarse con una rueda de la bici y una silla giratoria. La rueda y la persona en la silla constituyen un sistema con algún ímpetu angular. Si la persona aplica un esfuerzo de torsión para hacer girar la rueda con el eje apuntando verticalmente, el sistema habrá ganado ímpetu angular. Si la persona luego gira la rueda que hace girar, ella comenzará a girar en su silla en la dirección opuesta de la rueca. Aquí, el sistema tenía ímpetu angular, con su dirección se determina por la regla derecha. Cuando se gira la rueda, el ímpetu angular del sistema cambió la dirección. Debido a la conservación, la silla comenzó a gire en la dirección opuesta de modo que el ímpetu angular total del sistema era igual a la del sistema antes de la rueda fue movido de un tirón.
Otra demostración de la conservación del ímpetu angular puede hacerse con una silla giratoria y dos pesos. Si los pesos se celebran a lo largo del brazo mientras gira la silla y luego se traen cerca del pecho, habrá un aumento en la velocidad angular. Esto sucede porque llevar los pesos más el eje de rotación disminuye el momento de inercia del sistema. Si no actúa fuerza para hacer girar la silla, el esfuerzo de torsión en el sistema es cero. El ímpetu angular debe permanecer constante, no pares, y la única manera para que eso suceda es para que la velocidad angular aumentar.
En este experimento, una varilla giratoria está conectada a un peso descendente. El peso cae proporcionará una torsión en la barra, y el ímpetu angular se medirá en dos puntos: primero, cuando el peso ha caído a la mitad y luego otra vez una vez que el peso llega al final de la cadena. Vea la figura 1 para una imagen de la instalación experimental.
Es el momento de inercia de una barra de giro  , donde
, donde  es la masa de la varilla y
es la masa de la varilla y 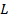 es la longitud. Estas cantidades se pueden medir antes de que el experimento lleva a cabo. Para encontrar la velocidad angular
es la longitud. Estas cantidades se pueden medir antes de que el experimento lleva a cabo. Para encontrar la velocidad angular  , se utilizarán las ecuaciones cinemáticas rotacionales:
, se utilizarán las ecuaciones cinemáticas rotacionales:
 . (Ecuación 3)
. (Ecuación 3)
Ecuación 3 indica que la velocidad angular final  es igual a la velocidad angular inicial
es igual a la velocidad angular inicial  además de la aceleración angular
además de la aceleración angular 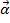 , multiplicado por el tiempo. Porque la varilla comenzará en reposo,
, multiplicado por el tiempo. Porque la varilla comenzará en reposo,  sea igual a cero. La aceleración angular
sea igual a cero. La aceleración angular 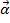 es definido por
es definido por 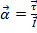 , donde
, donde  es el par y
es el par y  es el momento de inercia. El torque es la fuerza del peso que causa una tensión en la cadena, que hace que la barra girar, multiplicada por la distancia desde la fuerza hasta el eje de rotación:
es el momento de inercia. El torque es la fuerza del peso que causa una tensión en la cadena, que hace que la barra girar, multiplicada por la distancia desde la fuerza hasta el eje de rotación:  que la fuerza que actúa sobre la polea es igual a la fuerza sobre el peso:
que la fuerza que actúa sobre la polea es igual a la fuerza sobre el peso: 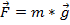 , donde
, donde  es la masa y
es la masa y  es la aceleración debido a la gravedad. El radio de
es la aceleración debido a la gravedad. El radio de  del esfuerzo de torsión será la distancia de la cuerda enrollada en el eje de rotación.
del esfuerzo de torsión será la distancia de la cuerda enrollada en el eje de rotación.

Figura 1. Disposición experimental. Detalle: soporte de anillo 1) grande, 2) extensor, conjunto 3) giratorio, 4) el peso y barra 5) par.
Procedimiento
1. prueba de la teoría de la conservación del ímpetu angular con la rueda de la bici.
- Mientras sentado en una silla que puede girar libremente, comenzar a girar la rueda de la bici y entonces la sujete por las asas hasta su dirección del ímpetu angular es vertical.
- Sosteniendo la rueda por las dos asas, voltea la rueda para que su momento angular apunta en la dirección opuesta. Observe cómo la Cátedra comenzará a girar.
2. prueba de la teoría de la conservación del ímpetu angular con dos pesos.
- Mientras estaba sentado en una silla que puede girar libremente, sostener dos pesos hacia fuera a lo largo del brazo.
- Tener un socio Haz el giro de la silla y luego acercan las pesas el pecho. Tenga en cuenta el aumento de la velocidad de rotación de la silla.
3. medir el cambio de ímpetu angular en la barra de giro.
- Mida la longitud de la varilla y su masa. Usando un palillo del metro medir el punto medio del caída de peso y marcar el rayo vertical con cinta adhesiva para tener una referencia. Calcular el momento de inercia de la varilla.
- Agregar 200 g al extremo de la cuerda y viento hasta la parte superior. Tener en cuenta donde se encuentra el punto medio de la cadena.
- Liberar el peso y medir la cantidad de tiempo que tarda en llegar a la marca a la mitad y luego otra vez a la parte inferior. Hacer esto tres veces y tomar los valores medios. Calcular el momento angular en ambos puntos.
- Aumentar el peso en el extremo de la cuerda para la 500 g y repetir el paso 3.3.
- Aumentar el peso de 1.000 g y repetir el paso 3.3.
Resultados
| Masa (g) |
Ímpetu angular en el medio /s (kg m2) |
Ímpetu angular en la parte inferior /s (kg m2) |
Diferencia /s (kg m2) |
| 200 | 0,41 | 0.58 | 0.17 |
| 500 | 0.66 | 0.91 | 0.25 |
| 1.000 | 0,93 | 1.32 | 0.39 |
En el primer paso, se confirmó la teoría de la conservación del ímpetu angular, la silla comenzó a girar cuando la rueda se volcó. En el paso dos, la teoría de la conservación del ímpetu angular fue otra vez confirmada, la silla comenzó a girar más rápido cuando los pesos fueron el momento de inercia del sistema se redujo. En el paso tres del laboratorio, el mayor esfuerzo de torsión en la barra de giro aumenta el ímpetu angular. Con todas las otras cantidades es constante, el ímpetu angular aumenta linealmente con el tiempo.
Aplicación y resumen
Al igual que en la parte de silla giratoria del lab, cambiando el momento de inercia de un objeto puede aumentar o disminuir la velocidad angular del objeto. Figura patinadores aprovechar esta a veces comience a pedalear con los brazos extendidos y entonces acercan sus armas sus cuerpos, que los harán girar mucho más rápido.
¿Por qué es más fácil equilibrio en una bicicleta cuando está en movimiento? La respuesta es ímpetu angular. Cuando no están girando las ruedas, es fácil para la bicicleta se caiga. Una vez que las ruedas están en movimiento, tienen cierta cantidad de momento angular. Cuanto mayor sea el ímpetu angular, el par más es necesario para cambiar, por lo que es más difícil volcar la moto.
Si un mariscal de campo jugando al fútbol le tira sin poner cualquier giro en la bola, su vuelo será inestable y podría perder su objetivo. Para evitar esto, mariscales de campo utilizan sus dedos para obtener el balompié de spinning cuando lanza. Cuando la bola gira cuando vuela por el aire, tiene ímpetu angular, que requiere de esfuerzo de torsión para cambiar la dirección del ímpetu angular. La bola se balancea ni dan la vuelta en el aire.
En este experimento, el concepto de conservación del ímpetu se probó en dos manifestaciones. En uno, la dirección del momento angular se conserva, y en la otra, la magnitud fue conservada. En la última parte del experimento, se midió el efecto de un esfuerzo de torsión en el momento angular.
Saltar a...
Vídeos de esta colección:

Now Playing
Momento angular
Physics I
36.3K Vistas

Las leyes del movimiento de Newton
Physics I
76.1K Vistas

Fuerza y aceleración
Physics I
79.3K Vistas

Vectores en múltiples direcciones
Physics I
182.5K Vistas

Cinemática y movimiento de proyectiles
Physics I
72.8K Vistas

Ley de la gravitación Universal de Newton
Physics I
191.7K Vistas

Conservación del momento
Physics I
43.4K Vistas

Fricción
Physics I
52.9K Vistas

Ley de Hooke y el movimiento armónico simple
Physics I
61.4K Vistas

Diagramas de equilibrio y de cuerpo libre
Physics I
37.4K Vistas

Esfuerzo torsional
Physics I
25.0K Vistas

Inercia rotacional
Physics I
43.6K Vistas

Energía y trabajo
Physics I
50.0K Vistas

Entalpía
Physics I
60.4K Vistas

Entropía
Physics I
17.7K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados